Representing and manipulating information

Relevant Reading

This lecture will cover contents from Chapter 4 of the book.

1. How do we “see” things?

1.2 Everything is a bit

• Each bit is 0 or 1

• By encoding/interpreting sets of bits in various ways

  • Computers determine what to do (instructions)

  • … and represent and manipulate numbers, sets, strings, etc…

• Why bits? Electronic Implementation

  • Easy to store with bistable elements.

  • Reliably transmitted on noisy and inaccurate wires.

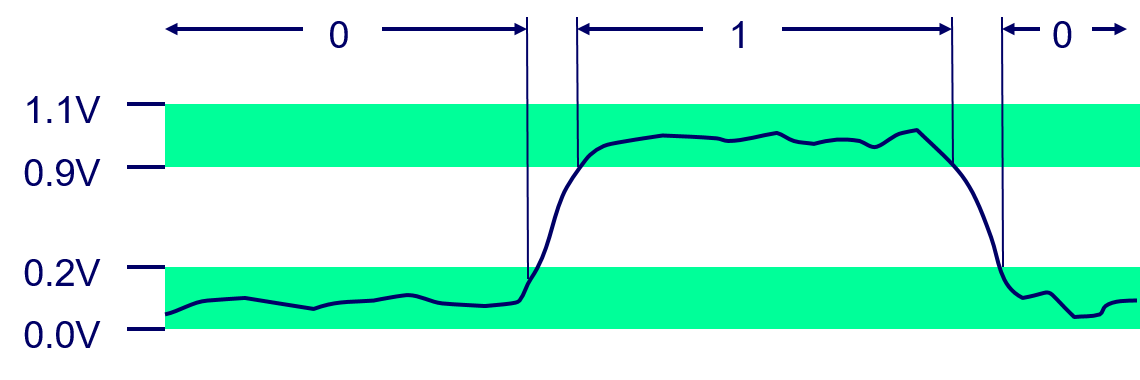
1.3 Encoding byte values

• Byte = 8 bits

• Binary: 0000 0000 to 1111 1111.

• Decimal: 0 to 255.

• Hexadecimal: 00 to FF.

  • Base 16 number representation

  • Use character 0 to 9 and A to F.

• Example: 15213 (decimal) = 0011 1011 0110 1101 (binary) = 3B6D (hex)

Hex	Decimal	Binary	Binary to Decimal Calculation
0	0	0000	0 * \(2^3\) + 0 * \(2^2\) + 0 * \(2^1\) + 0 * \(2^0\)
1	1	0001	0 * \(2^3\) + 0 * \(2^2\) + 0 * \(2^1\) + 1 * \(2^0\)
2	2	0010	0 * \(2^3\) + 0 * \(2^2\) + 1 * \(2^1\) + 0 * \(2^0\)
3	3	0011	0 * \(2^3\) + 0 * \(2^2\) + 1 * \(2^1\) + 1 * \(2^0\)
4	4	0100	0 * \(2^3\) + 1 * \(2^2\) + 0 * \(2^1\) + 0 * \(2^0\)
5	5	0101	0 * \(2^3\) + 1 * \(2^2\) + 0 * \(2^1\) + 1 * \(2^0\)
6	6	0110	0 * \(2^3\) + 1 * \(2^2\) + 1 * \(2^1\) + 0 * \(2^0\)
7	7	0111	0 * \(2^3\) + 1 * \(2^2\) + 1 * \(2^1\) + 1 * \(2^0\)
8	8	1000	1 * \(2^3\) + 0 * \(2^2\) + 0 * \(2^1\) + 0 * \(2^0\)
9	9	1001	1 * \(2^3\) + 0 * \(2^2\) + 0 * \(2^1\) + 1 * \(2^0\)
A	10	1010	1 * \(2^3\) + 0 * \(2^2\) + 1 * \(2^1\) + 0 * \(2^0\)
B	11	1011	1 * \(2^3\) + 0 * \(2^2\) + 1 * \(2^1\) + 1 * \(2^0\)
C	12	1100	1 * \(2^3\) + 1 * \(2^2\) + 0 * \(2^1\) + 0 * \(2^0\)
D	13	1101	1 * \(2^3\) + 1 * \(2^2\) + 0 * \(2^1\) + 1 * \(2^0\)
E	14	1110	1 * \(2^3\) + 1 * \(2^2\) + 1 * \(2^1\) + 0 * \(2^0\)
F	15	1111	1 * \(2^3\) + 1 * \(2^2\) + 1 * \(2^1\) + 1 * \(2^0\)

• Google Spreadsheet demonstrating conversion process

1.4 How are data represented?

C data type	typical 32-bit	typical 64-bit	x86_64
char	1	1	1
short	2	2	2
int	4	4	4
long	4	8	8
float	4	4	4
double	8	8	8
pointer	4	8	8

2. Bit-level operations in C

• Boolean algebra developed by George Boole in 19th century

• Algebraic representation of logic: encode True as 1 and False as 0.

• Operations: AND (&), OR (|), XOR (^), NOT (~).

A	B	A&B	A|B	A^B	~A
0	0	0	0	0	1
0	1	0	1	1	1
1	0	0	1	1	0
1	1	1	1	0	0

• General Boolean algebra

  • Operate on bit vectors

  • Operation applied bitwise.

  • All properties of boolean algebra apply.

• Operation and notation

  • Boolean operations: &, |, ^, ~.

  • Shift operations:

    • Left Shift: x << y

      • Shift bit-vector x left y positions

      • Throw away extra bits on left

      • Fill with 0’s on right

    • Right Shift: x >y

      • Shift bit-vector x right y positions

      • Throw away extra bits on right

      • Logical shift (for unsigned values)

        • Fill with 0’s on left

      • Arithmetic shift (for signed values)

        • Replicate most significant bit on left

    • Undefined Behavior

      • Shift amount < 0 or ≥ word size

  • Apply to any “integral” data type: long, int, short, char, unsigned

  • View arguments as bit vectors.

  • Arguments applied bit-wise.

  • Mathematical operations:

    • Bit-wise with carry

    • \(0 + 0 = 0\)

    • \(0 + 1 = 1\)

    • \(1 + 0 = 1\)

    • \(1 + 1 = 0\) and carry \(1\) to the next bit operation (or add 1 to left of the most significant bit position)

Hands-on: bit-level operations in C

• Inside your csc231, create another directory called 03-data and change into this directory.

• Create a file named bitwise_demo.c with the following contents:

• Compile and run bitwise_demo.c.

• Confirm that the binary printouts match the corresponding decimal printouts and the expected bitwise operations.

3. Encoding integers

3.1 Mathematical equation

• Assumption:

  • \(X\) is a decimal number

  • \(X\) can be represented using \(w\) bits under the form \(x_{w-1}x_{w-2}...x_{i}...x_{1}x_{0}\).

  • \(x_i\) is a binary value at bit position \(i\) with \(0\leq i \leq (w - 1)\)

• The mathematical equation governing the encoding from an unsigned value of \(X\) into a sequence of binary values \(x_{w-1}x_{w-2}...x_{i}...x_{1}x_{0}\) is:

\(X=\sum_{i=0}^{w-1}x_{i}*2^{i}\)

3.2 What about negative numbers?

• Approaches:

  • Reserve first bit as sign bit

  • One’s complement: The addition of a negative number and its corresponding positive value (complement) in an N-bit binary representation will result in a binary representation that has N ones.

    • For example: in a 3-bit representation, \(2\) is represented as 010, and \(-2\) is represented as 101. Then, \(2+(-2)\) becomes \(010+101=111\).

  • Two’s complement: The addition of a negative number and its corresponding positive value (‘complement) in  an N-bit` binary representation will a binary representation of to \(2^N\).

    • For example: in a 3-bit representation, \(3\) is represented as 011 and \(-3\) is represented as 101. The sum of these two binary representations is 1000, which is the binary representation of \(2^3\).

• Two’s complement is preferred in modern computing design as it supports fundamental arithmetic operations of addition, subtraction, and multiplication of integer numbers as if these numbers were positive.

• The mathematical equation governing the encoding from a signed value of \(X\) into a 2’s complement sequence of binary values \(x_{w-1}x_{w-2}...x_{i}...x_{1}x_{0}\) is:

\(X=-x_{w-1} * 2^{w-1} + \sum_{i=0}^{w-2}x_{i}*2^{i}\)

• For 2’s complement, most significant bit indicates sign.

  • 0 for nonnegative

  • 1 for negative

Unsigned	Binary	2’s complement	1’s complement
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	8	-7
9	1001	-7	-6
10	1010	-6	-5
11	1011	-5	-4
12	1100	-4	-3
13	1101	-3	-2
14	1110	-2	-1
15	1111	-1	0

• C does not mandate using 2’s complement.

  • But, most machines do, and we will assume so.

	Decimal	Hex	Binary
short int x	15213	3B 6D	00111011 01101101
short int y	-15213	C4 93	11000100 10010011

2’s complement examples

• 2’s complement representation depends on the number of bits.

• Technical trick: A binary representation of the absolute value of negative 2 to the power of the number of bits minus the absolute value of the negative number.

• Simple example for 5-bit representation

	-16	8	4	2	1
10	0	1	0	1	0	8 + 2 = 10
-10	1	0	1	1	0	-16 + 4 + 2 = -10

• Simple example for 6-bit representation

	-32	16	8	4	2	1
10	0	0	1	0	1	0	8 + 2 = 10
-10	1	1	0	1	1	0	-32 + 16 + 4 + 2 = -10

• Complex example

	Decimal	Hex	Binary
short int x	15213	3B 6D	00111011 01101101
short int y	-15213	C4 93	11000100 10010011

Weight	15213		-15213
1	1	1	1	1
2	0	0	1	2
4	1	4	0	0
8	1	8	0	0
16	0	0	1	16
32	1	32	0	0
64	1	64	0	0
128	0	0	1	128
256	1	256	0	0
512	1	512	0	0
1024	0	0	1	1024
2048	1	2048	0	0
4096	1	4096	0	0
8192	1	8192	0	0
16384	0	0	1	16384
-32768	0	0	1	-32768
——	—–	—–	——	——
Sum		15213		-15213

3.3 Numeric ranges

• Unsigned values for w-bit word

  • UMin = 0

  • UMax = \(2^{w} - 1\)

• 2’s complement values for w-bit word

  • TMin = \(-2^{w-1}\)

  • TMax = \(2^{w-1} - 1\)

  • -1: 111..1

• Values for different word sizes:

	8 (1 byte)	16 (2 bytes)	32 (4 bytes)	64 (8 bytes)
UMax	255	65,535	4,294,967,295	18,446,744,073,709,551,615
TMax	127	32,767	2,147,483,647	9,223,372,036,854,775,807
TMin	-128	-32,768	-2,147,483,648	-9,223,372,036,854,775,808

• Observations

  • abs(TMin) = TMax + 1

    • Asymetric range

  • UMax = 2 * TMax + 1

• C programming

  • #include <limits.h>

  • Declares constants: ULONG_MAX, LONG_MAX, LONG_MIN

  • Platform specific

Challenge

• Write a C program called numeric_ranges.c that prints out the value of ULONG_MAX, LONG_MAX, LONG_MIN. Also answer the following question: If we multiply LONG_MIN by -1, what do we get?

• Note: You need to search for the correct format string specifiers.

Solution

-p allows the creation of all directories on the specified path, regardless whether any directory on that path exists.

4. Conversions (casting)

What does it really mean by casting

• C allows casting between different numeric data types.

• What should be the effect/impact?

• Notations:

  • B2T: Binary to 2’s complement

  • B2U: Binary to unsigned

  • U2B: Unsigned to binary

  • U2T: Unsigned to 2’s complement

  • T2B: 2’s complement to binary

  • T2U: 2’s complement to unsigned

Visualization of conversions

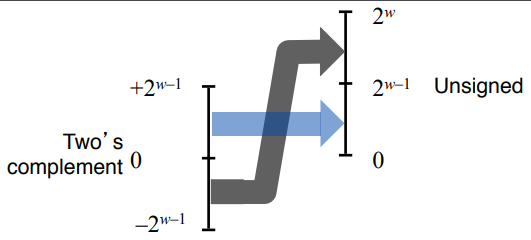
• \(T2U_{w}(x) = x + 2^{w} \ if \ x < 0\)

• \(T2U_{w}(x) = x \ if \ x \geq 0\)

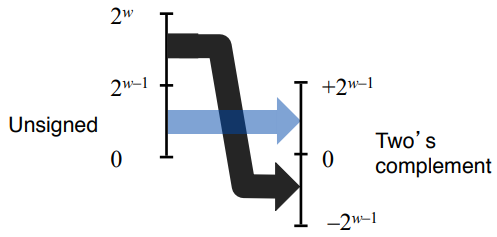
• \(U2T_{w}(x) = x - 2^{w} \ if x > TMax_{w}\)

• \(U2T_{w}(x) = x \ if \ x \leq TMax_{w}\)

• Summary

  • Bit pattern is maintained but reinterpreted

  • Can have unexpected effects: adding or subtracting 2^w

  • When expressions contain both signed and unsigned int values, int values will be casted to unsigned.

Hands on: casting

• Create a file named casting.c with the following contents:

• Compile and run casting.c.

• Confirm that converted values are correct.

Challenge

• What is wrong with the following program?

• How can this program be corrected?

Solution

• Change the range to 11-1

• Why don’t we change the type of i? that path exists.

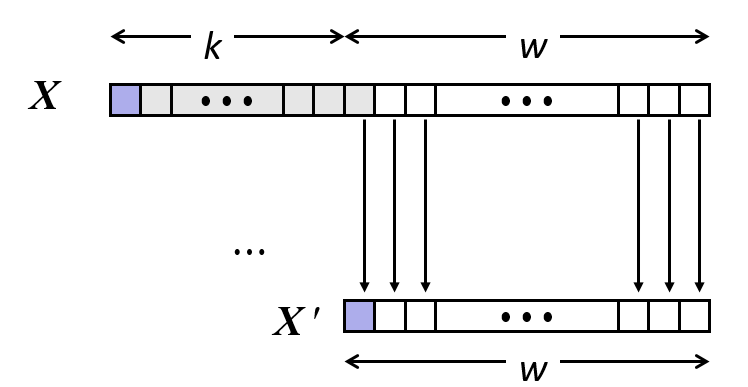
Expanding and truncation

• Expanding (e.g., short int to int)

  • Unsigned: zeros added

  • Signed: sign extension

  • Both yield expected result

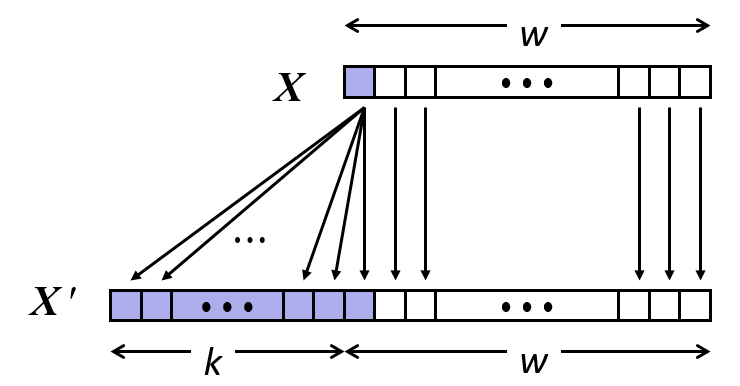
• Truncating (e.g., unsigned to unsigned short)

  • Unsigned/signed: bits are truncated

  • Result reinterpreted

  • Unsigned: mod operation

  • Signed: similar to mod

  • For small (in magnitude) numbers yields expected behavior

Misunderstanding integers can lead to the end of the world!

• Thule Site J: USAF radar station for missile warning and spacecraft tracking.

• “There are many examples of errors arising from incorrect or incomplete specifications. One such example is a false alert in the early days of the nuclear age, when on October 5, 1960, the warning system at NORAD indicated that the United States was under massive attack by Soviet missiles with a certainty of 99.9 percent. It turned out that the Ballistic Missile Early Warning System (BMEWS) radar in Thule, Greenland, had spotted the rising moon. Nobody had thought about the moon when specifying how the system should act.” (Computer System Reliability and Nuclear War, CACM 1987).

• Moon’s large size: 1000s of objects reported.

• Moon’s distance: .25 million miles

  • Thule’s BMEWS max distance: 3000 miles.

  • Truncated distance to the moon: % sizeof(distance) = 2200 miles.

• Remember assignment 1: The computer does not “see”, it only interprets.

  • Thousands of objects on the sky within missile detection range!.

• Human control:

  • Kruschev was in New York on October 5, 1960.

  • Someone at Thule said, “why not go check outside?”

5. Addition, multiplication, and negation (of integers)

Binary addition

• Mathematical operations:

  • Bit-wise with carry

  • \(0 + 0 = 0\)

  • \(0 + 1 = 1\)

  • \(1 + 0 = 1\)

  • \(1 + 1 = 0\) and carry \(1\) to the next bit operation (or add 1 to left of the most significant bit position)

• This works for both unsigned and 2’s complement notation

• Example 1: 4-bit unsigned \(2+6=8\)

\[\begin{split} \ 0010 \\ +\ 0110 \\ \hline \ 1000 \end{split}\]

• Example 2: 4-bit unsigned \(11+12=23\)

\[\begin{split} \ 1011 \\ +\ 1100 \\ \hline \ 10111 \end{split}\]

• Example 3: 4-bit signed \(5-7=5+(-7)=(-2)\)

  • Positive to negative conversion in 2’s complement: flipped bit and add 1.

  • \(7\): \(0111\)

  • \(-7\): \(1000 + 1=1001\)

\[\begin{split} \ 0101 \\ +\ 1001 \\ \hline \ 1110 \end{split}\]

\(1110=(-1)*(1)*(8)+(1)*(4)+(1)*(2)+(0)*1)=(-8)+4+2=(-2)\)

Unsigned addition

• Given w bits operands

• True sum can have w + 1 bits (carry bit).

• Carry bit is discarded.

• Implementation:

• s = (u + v) mod 2^w

Hands on: unsigned addition

• Create a file named unsigned_addition.c with the following contents:

• Compile and run unsigned_addition.c.

• Confirm that calculated values are correct.

2’s complement addition

• Almost similar bit-level behavior as unsigned addition

  • True sum of w-bit operands will have w+1-bit, but

  • Carry bit is discarded.

  • Remainding bits are treated as 2’s complement integers.

• Overflow behavior is different

• \(TAdd_{w}(u, v) = u + v + 2^{w}\) if \(u + v < TMin_{w}\) (Negative Overflow)

• \(TAdd_{w}(u, v) = u + v\) if \(TMin_{w} \leq u + v \leq TMax_{w}\)

• \(TAdd_{w}(u, v) = u + v - 2^{w}\) if \(u + v TMax_{w}\) (Positive Overflow)

Hands on: signed addition

• Create a file named signed_addition.c with the following contents:

• Compile and run signed_addition.c.

• Confirm that calculated values are correct.

Multiplication

• Compute product of w-bit numbers x and y.

• Exact results can be bigger than w bits.

  • Unsigned: up to 2w bits: \(0 \leq x * y \leq (2^{w} - 1)^{2}\)

  • 2’s complement (negative): up to 2w - 1 bits: \(x * y \geq (-2)^{2w-2} + 2^{2w-1}\)

  • 2’s complement (positive): up to 2w bits: \(x * y \leq 2^{2w-2}\)

• To maintain exact results:

  • Need to keep expanding word size with each product computed.

  • Is done by software if needed (arbitrary precision arithmetic packages).

• Trust your compiler: Modern CPUs and OSes will most likely know to select the optimal method to multiply.

Multiplication and Division by power-of-2

• Power-of-2 multiply with left shift

  • \(u << k\) gives \(u * 2^{k}\)

  • True product has w + k bits: discard k bits.

• Unsigned power-of-2 divide with right shift

  • \(u >> k\) gives \(floor(u / 2^{k})\)

  • Use logical shift.

• Signed power-of-2 divide with shift

  • x > 0: \(x >> k\) gives \(floor(u / 2^{k})\)

  • x < 0: \((x + (1 << k) - 1) >> k\) gives ceiling \(u / 2^{k}\)

  • C statement: (x < 0 ? x + (1 << k) - 1: x) >k

Negation: complement and increase

• Negate through complement and increment:

  • ~x + 1 == -x

Challenge

• Implement a C program called negation.c that implements and validates the equation in slide 24. The program should take in a command line argument that takes in a number of type short to be negated.

• What happens if you try to negate -32768?

Solution

6. Byte-oriented memory organization

Overview

• Programs refer to data by address

  • Conceptually, envision it as a very large array of bytes

    • In reality, it’s not, but can think of it that way

  • An address is like an index into that array

    • and, a pointer variable stores an address

• Note: system provides private address spaces to each “process”

  • Think of a process as a program being executed

  • So, a program can clobber its own data, but not that of others

Machine words

• Any given computer has a “Word Size”

• `word size”: Nominal size of integer-valued data and of addresses

• Until recently, most machines used 32 bits (4 bytes) as word size

  • Limits addresses to 4GB (232 bytes)

• Increasingly, machines have 64-bit word size

  • Potentially, could have 18 EB (exabytes) of addressable memory

  • That’s 18.4 X 1018

• Machines still support multiple data formats

  • Fractions or multiples of word size

  • Always integral number of bytes

Word-oriented memory organization

• Addresses specific byte locations

  • Address of first byte in word.

  • Address of successive words differ by 4 (32-bit) or 8 (64-bit).

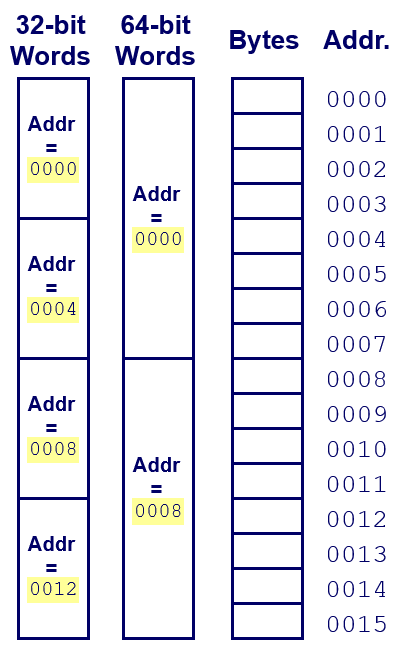
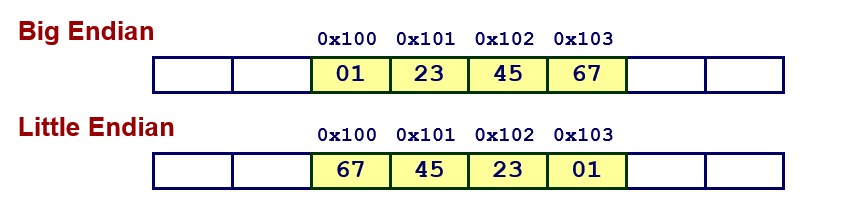
Byte ordering in memory

• Machine-dependent

• Big Endian: Sun (Oracle SPARC), PPC Mac, Internet (network data transfer)

  • Least significant byte has the highest address.

• Little Endian: x86, ARM processors running Android, iOS, and Linux

  • Least significant byte has lowest address.

• Example

  • Variable x has 4-byte value of 0x01234567

  • Address given by &x is 0x100

Hands on: byte ordering in memory

• Make sure that you are inside 03-data directory.

• Create a file named byte_ordering.c with the following contents:

• Compile and run byte_ordering.c.

• Confirm that calculated values are correct.

7. Fractional binary numbers (float and double)

Naive representation

• What is 1011.101₂?

  • 8 + 0 + 2 + 1 + 1/2 + 0 + 1/4

• Can only exactly represent numbers of the form x/2^k

• Limited range of numbers within the w-bit word size.

IEEE Floating point

• IEEE Standard 754

  • Established in 1985 as uniform standard for floating point arithmetic

  • Supported by all major CPUs

  • Some CPUs don’t implement IEEE 754 in full, for example, early GPUs, Cell BE processor

• Driven by numerical concerns

  • Nice standards for rounding, overflow, underflow

  • Hard to make fast in hardware (Numerical analysts predominated over hardware designers in defining standard).

Importance of floating-point arithmetic accuracy

• Ariane 5 explordes on maiden voyage: $500 million dollars lost.

  • 64-bit floating point number assigned to 16-bit integer

  • Cause rocket to get incorrect value of horizontal velocity and crash.

• Patriot Missle defense system misses Scud: 28 dead

  • Velocity is a real number that can be expressed as a whole number and a decimal (e.g., 3750.2563…miles per hour). Time is kept continuously by the system’s internal clock in tenths of seconds but is expressed as an integer or whole number (e.g., 32,33, 34…). The longer the system has been running, the larger the number representing time. To predict where the Scud will next appear, both time and velocity must be expressed as real numbers. Because of the way the Patriot computer performs its calculations and the fact that its registers are only 24 bits long, the conversion of time from an integer to a real number cannot be any more precise than 24 bits. This conversion results in a loss of precision causing a less accurate time calculation. The effect of this inaccuracy on the range gate’s calculation is directly proportional to the target’s velocity and the length of time the system has been running. Consequently, performing the conversion after the Patriot has been running continuously for extended periods causes the range gate to shift away from the center of the target, making it less likely that the target, in this case a Scud, will be successfully intercepted.

IEEE Floating point representation

• Numerical form: (-1)^sM2^E

  • Sign bit s determins whether the number is negative or positive.

  • Significant M normalizes a fractional value in range [1.0, 2.0).

  • Exponent E weights value by power of two.

• Encoding

  • Most significant bit is sign bit s.

  • exp field encodes E (but is not equal to E)

  • frac field encodes M (but is not equalt to M)

• Single precision: 32 bits

• Double precision: 64 bits

Three “kinds” of floating point numbers

• Depends on the exp field (E).

• Denormalized: exp contains all 0s.

• Special: exp contains all 1s.

• Normalized: exp contains a mix of 0s and 1s.

Normalized floating point numbers

• When: exp != 000…0 and exp != 111…1

• Exponent coded as a biased value: E = exp – Bias

  • exp: unsigned value of exp field

  • \(Bias = 2^{k-1} - 1\), where k is number of exponent bits

    • Single precision: 127 (exp: 1…254, E: -126…127)

    • Double precision: 1023 (exp: 1…2046, E: -1022…1023)

• Significand coded with implied leading 1: M = 1.xxx…x₂

  • xxx…x: bits of frac field

  • Minimum when frac=000…0 (M = 1.0)

  • Maximum when frac=111…1 (M = 2.0 – ε)

  • Get extra leading bit for “free” (hence the range: [1.0, 2.0))

Example: normalized floating point numbers

• Value: float F = 15213.0;

  • 15213₁₀= 11101101101101₂= 1.1101101101101₂* 2¹³

• Significand:

  • M = 1.1101101101101₂

  • frac = 11011011011010000000000₂

• Exponent:

  • E = 13

  • Bias = 127

  • exp = 140 = 10001100₂

• Result: 0|10001100|11011011011010000000000

Hands on: check floating point representation

• Make sure that you are inside 03-data directory.

• Create a file named show_fp.c with the following contents:

• Compile and run show_fp.c.

• Confirm that calculated values in the previous example are correct.

Denormalized floating point

• Condition: exp = 000…0

• Exponent value: E = 1 – Bias

• Significand coded with implied leading 0: M = 0.xxx…x₂

  • xxx…x: bits of frac

• Cases

  • exp = 000…0, frac = 000…0

    • Represents zero value

    • Note distinct values: +0 and –0

  • exp = 000…0, frac ≠ 000…0

    • Numbers closest to 0.0

    • Equispaced

Special cases

• Condition: exp = 111…1

• Case: exp = 111…1, frac = 000…0

  • Represents value infinity

  • Operation that overflows

  • Both positive and negative

• Case: exp = 111…1, frac != 000…0

  • Not-a-Number (NaN)

  • Represents case when no numeric value can be determined

8. Floating operations

Basic idea

• Compute exact result.

• Make it fit into desired precision.

  • Possible overflow if exponent too large

  • Possible round to fit into frac

• Rounding modes

	1.40	1.60	1.50	2.50	-1.50
Towards zero	1	1	1	2	-1
Round down	1	1	1	2	-2
Round up	2	1	1	3	-1
Nearest even (default)	1	2	2	2	-2

• Nearest even

  • Hard to get any other mode without dropping into assembly.

  • C99 has support for rounding mode management

• All others are statistically based

  • Sum of set of positive numbers will consistently be over- or under-estimated.

Floating point multiplication

• \((-1)^{s_1}M_{1}2^{E_1} * (-1)^{s_2}M_{2}2^{E_2}\)

• Exact result: \((-1)^{s}M2^{E}\)

  • \(s = s_{1} XOR s_{2}\)

  • \(M = M_{1}*M_{2}\)

  • \(E = E_{1}+E_{2}\)

• Correction

  • If M >= 2, shift M right, increment E.

  • If E out of range, overflow.

  • Round M to fit frac precision

• Implementation: Biggest chore is multiplying significands.

Floating point addition

• \((-1)^{s_1}M_{1}2^{E_1} + (-1)^{s_2}M_{2}2^{E_2}\)

• Exact result: \((-1)^{s}M2^E\)1

  • Sign s, significand M: result of signed align and add

  • E = E₁

• Correction

  • If M >= 2, shift M right, increment E.

  • If M < 1, shift M left k positions, decrement E by k.

  • Overflow if E out of range

  • Round M to fit frac precision

• Implementation: Biggest chore is multiplying significands.

Mathematical properties of floating point addition

• Compare to those of Abelian group (a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written):

  • Closed under addition? Yes (but may generate infinity or NaN)

  • Communicative? Yes

  • Associative? No

    • Overflow and inexactness of rounding

    • (3.14+1e10)-1e10 = 0, 3.14+(1e10-1e10) = 3.14

  • 0 is additive identity? Yes

  • Every element has additive inverse? Almost

    • Except for infinities and NaN

• Monotonicity?

  • Almost

  • Except for infinities and NaN

Mathematical properties of floating point multiplication

• Compare to those of Abelian group (a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written):

  • Closed under addition? Yes (but may generate infinity or NaN)

  • Communicative? Yes

  • Associative? No

    • Overflow and inexactness of rounding

    • (1e20 * 1e20) * 1e-20= inf, 1e20 * (1e20 * 1e-20)= 1e20

  • 1 is multiplicative identity? Yes

  • Multiplication distributes over addition? No

    • Overflow and inexactness of rounding

    • 1e20 * (1e20-1e20)= 0.0, 1e20 * 1e20 – 1e20 * 1e20 = NaN

• Monotonicity?

  • Almost

  • Except for infinities and NaN

Floating point in C

• C guarantees two levels

  • float: single precision

  • double: double precision

• Conversion/casting

  • Casting between int, float, and double changes bit representation

  • double/float to int

    • Truncates fractional part

    • Like rounding toward zero

    • Not defined when out of range or NaN: Generally sets to TMin

  • int to double

    • Exact conversion, as long as int has ≤ 53 bit word size

  • int to float

    • Will round according to rounding mode