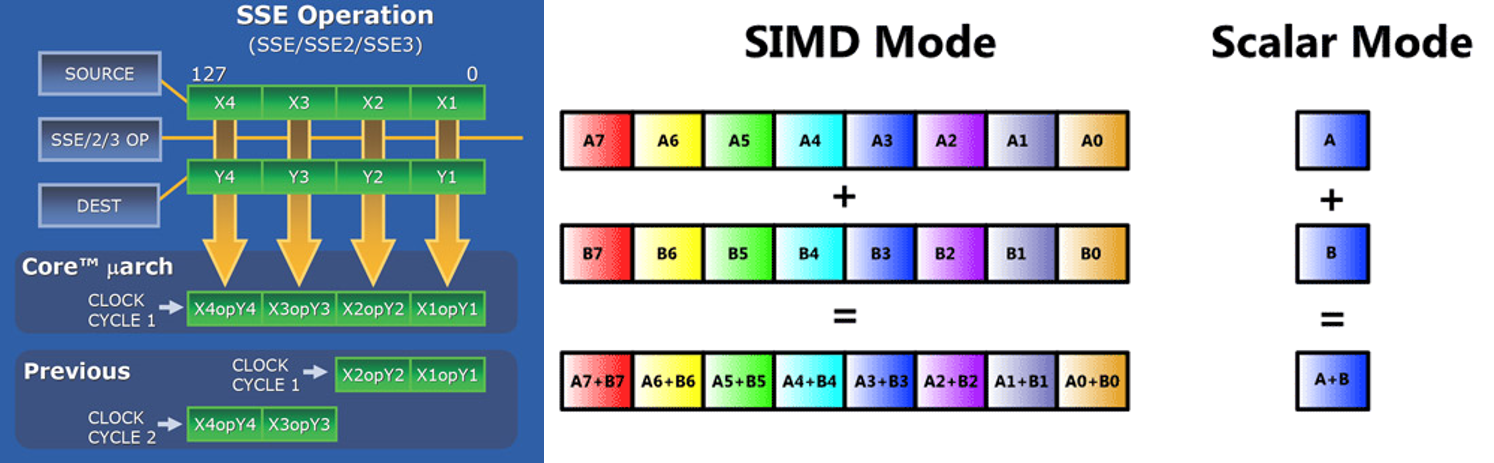
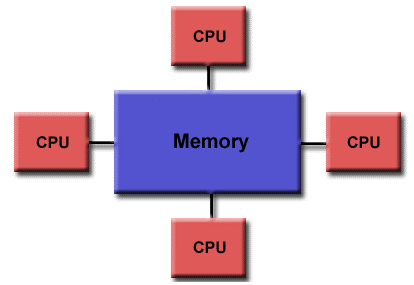
Introduction to paralel and distributed computing#

1. A simple computation problem#

Final GPA calculation
Components of a computation problem

  • Computational task

  • Execution framework.

  • Computing resources.

Computational tasks should be able to …

  • Be borken apart into discrete pieces of work that can be solved simultaneously.

  • Be solved in less time with multiple computing resources than with a single computing resource.

Execution framework should be able to …

  • Execute multiple program instructions concurrently at any moment in time

Computing resources might be …

  • A single computer with multiple processors.

  • An arbitrary number of computers connected by a network.

  • A special computational component inside a single computer, separate from the main processors (GPU), or

  • Any combintations of the above.

Parallelizing final GPA calculations

2. Parallel and distributed computing systems#

Definition

A collection of individual computing devices that can communicate with each other. (Attiya and Welch, 2004)

Emphasis …

A collection of individual computing devices that can communicate with each other. (Attiya and Welch, 2004)

How do parallel and distributed computing resources evolve?

  • Single site, single computer, single core

  • Single site, single computer, multiple cores

  • Single site, multiple computers, multiple cores

    • Cluster computing

  • Multiple sites, multiple computers, multiple cores, federated domains

    • Grid computing

  • Multiple site, multiple computers, multiple cores, virtula unified domain

    • Cloud computing

3. Can we just throw more computers at the problem?#

Definitions

  • Parallel speedup: how much faster the program becomes once some computing resources are added.

  • Parallel efficiency: Ratio of performance improvement per individual unit of computing resource.

Parallel speedup

  • Given p processors,

  • Speedup, S(p), is the ratio of the time it takes to run the program using a single processor over the time it takes to run the program using p processors.

  • The time it takes to run the program using a single processor, \(t_{s}\): sequential run time

  • The time it takes to the the program using multiple processor, \(t_{p}\): parallel run time

\(S(p) = \frac{sequential\ run\ time}{parallel\ run\ time} = \frac{t_s}{t_p}\)

Example 01

A program takes 30 seconds to run on a single-core machine and 20 seconds to run on a dual-core machine. What is the speedup of this program?

Solution

\(t_s=30\) \(t_p=20\)
\(S=\frac{t_s}{t_p}=\frac{30}{20}=1.5\)

Theoretical max

  • Let f be the fraction of the program that is not parallelizable.

  • Assume no overhead.

  • Running the program using one processor will take time \(t_s\).

  • The parallel run time, \(t_p\), can be calculated as the time it take to run the fraction that is non-parallelizable (\(f\times t_s\)) plus the remainning parallelizable fraction (\(1-f\)).

  • If \(p=1\), this simplifies to \(t_p=f\times t_s + (1-f)\times t_s\).

  • Assume no overhead, this means that we reduce the speed by half as we double the number of processor.

  • And so on …

scaling number of processors
Amdahl’s Law

  • This brings us to Amdahl’s Law, which quantifies speedup in term of number of processors and fraction of non-parallelizable code:

\(S(p)=\frac{t_s}{t_p}=\frac{t_s}{f\times t_s + (1-f)\times t_s}=\frac{1}{f + \frac{1-f}{p}}=\frac{p}{f \times (p-1) + 1}\)

Parallel efficiency

  • The efficiency E is then defined as the ratio of speedup S(p) over the number of processors p.

\(E=\frac{\frac{p}{f \times (p-1) + 1}}{p}=\frac{1}{f \times (p-1) + 1}\)

  • E is often measured as percentage.

  • For example, E = 0.8 means the parallel efficiency is 80%.

Example 02

Suppose that 4% of my application is serial. What is my predicted speedup according to Amdahl’s Law on 5 processors?

Solution

\(f=0.04\)

\(p=5\)

\(S=\frac{p}{(p-1)f + 1}=\frac{5}{4 \times 0.04 +1}=4.3103\)

Example 03

Suppose that I get a speedup of 8 when I run my application on 10 processors. According to Amdahl’s Law:

What portion of my code is serial?

\(S=8\)

\(p=10\)

\(S=\frac{p}{(p-1)f + 1}\)

\(8=\frac{10}{9f+1}\)

\(9f + 1 = \frac{10}{8}\)

\(f=\frac{1}{36}\)

What is the speedup on 20 processors?

\(f=\frac{1}{36}\)

\(p=20\)

\(S_{20}=\frac{p}{(p-1)f + 1}=\frac{20}{\frac{19}{36}+1} \approx 13.0909\)

What is the efficiency on 5 processors? 20 processors?

\(E=\frac{1}{(p-1)f + 1}\)

\(E_5=\frac{1}{\frac{4}{36}+1} = 90\% \)

\(E_{20}=\frac{1}{\frac{19}{36} + 1} \approx 65.45\% \)

What is the best speedup that I could achieve?

\(f=\frac{1}{36}\)

\(S_{\infty}=\lim_{p \to +\infty} \frac{p}{(p-1)f + 1} = \lim_{p \to +\infty} \frac{1}{\frac{p}{p-1}f + \frac{1}{p}}=\frac{1}{f}\)

\(S_{\infty}= 36\)

  • In other word, the highest number of processors one should add to this problem is 36.

Limiting factors of parallel speedup

  • Non-parallelizable code.

  • Communication overhead.

If there is no limiting factor …

  • 0% non-paralellizable code.

  • No communication overhead.

\(S_{\infty}=\lim_{f \to 0} \frac{p}{(p-1)f + 1} = p\)

\(S \leq p\)

Superlinear speedup

  • The unicorn of parallel and distributed computing.

  • Poor sequential reference implementation.

  • Memory caching.

  • I/O blocking.

4. Parallel and distributed computing system architectures#

Types of distributed computing systems

  • Streaming SIMD extensions for x86 architectures.

  • Shared memory.

  • Distributed shared memory.

  • Heterogeneous computing (accelerators).

  • Message passing.

Streaming SIMD
Streaming SIMD
Shared memory

  • One processor, multiple threads.

  • All threads have read/write access to the same memory.

  • Programming models:

    • Threads (pthread) - programmer manages all parallelism.

    • OpenMP: compiler extensions handle.

    • Vendor libraries: (Intel MKL - math kernel libraries)

shared memory
Heterogeneous computing

  • GPU

  • FPGA

  • Co-processors

GPU - graphics processing unit

  • Processor unit on graphic cards designed to support graphic rendering (numerical manipulation).

  • Significant advantage for certain classes of scientific problems.

  • Programming models:

    • CUDA: Library developed by NVIDIA for their GPUs.

    • OpenACC: Standard developed by NVIDIA, Cray, and Portal Compiler (PGI).

    • OpenAMP: Extension to Visual C++ to direct computation to GPU.

    • OpenCL: Public standard by the group the developed OpenGL.

GPU
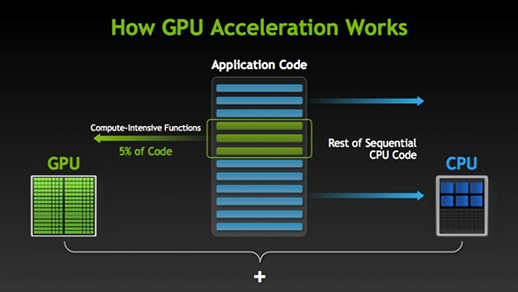
FPGA - field programmable array

  • Dynamically reconfigurable circuit board.

  • Expensive, difficult to program.

  • Power efficient, low heat.

Co-processors

  • Enables offloading of computationally intensive tasks from main CPU.

  • Similar to GPU, but can support a wider range of computational tasks.

  • Intel

    • Xeon Phi processor line.

    • PCIe-based add-on cards, but could also be used as a stand alone CPU.

    • Unlike GPU, Intel Xeon supports all programs targeted to standard x86 CPU (very minor modification if any)

Message passing distributed computing

  • Processes handle their own memory.

  • Data is passed between processes via messages.

    • Scales well.

    • Cluster can be built from commodity parts.

    • Cluster can easily be expanded.

    • Cluster can be heterogeneous.

  • Programming models:

    • MPI: standardized message passing library.

    • MPI + OpenMP: hybrid model.

    • MapReduce programming model for big data processing.

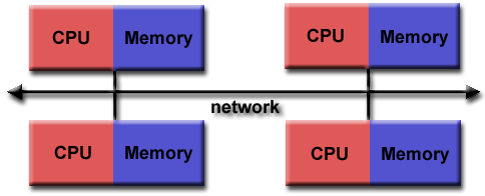
message passing

5. Benchmarking#

Benchmarking suites

  • LINPACK (Linear Algebra Package): Dense Matrix Solver

  • HPCC: High-Performance Computing Challenge.

    • HPL (LINPACK to solve linear system of equations)

    • DGEMM (Double precision general matrix multiply)

    • STREAM (Memory bandwidth)

    • PTRANS (Parallel matrix transpose to measure processors communication)

    • RandomAccess (random memory updates)

    • FFT (double precision complex discrete fourier transform)

    • Communication bandwidth and latency

  • SHOC: Scalable heterogeneous computing

    • Non-traditional system (GPU)

  • TestDFSIO

    • I/O performance of MapReduce/Hadoop Distributed File System.

Ranking systems

  • TOP500: Rank the supercomputers based on their LINPACK score.

  • GREEN500: Rank the supercomputers with emphasis on energy usage (LINPACK/power consumption).

  • GRAPH500: Rank systems based on benchmarks designed for data-intensive computing.