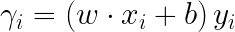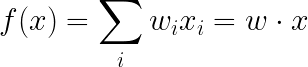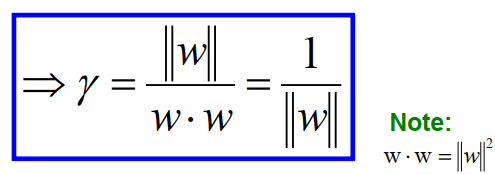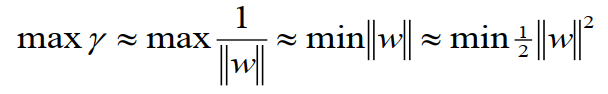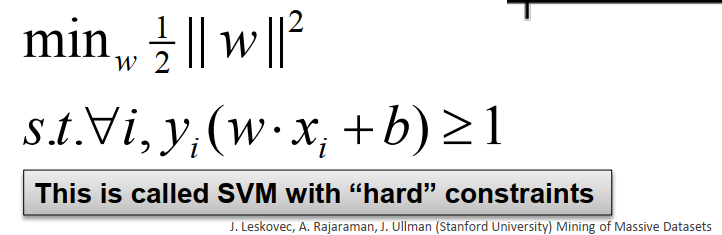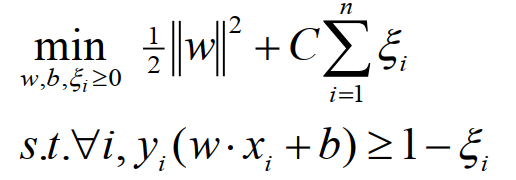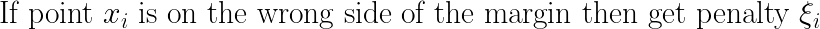Distributed machine learning with Spark#

1. Application: Spam Filtering#

viagra

learning

the

dating

nigeria

spam?

X1

1

0

1

0

0

y1 = 1

X2

0

1

1

0

0

Y2 = -1

X3

0

0

0

0

1

y3 = 1

  • Instance spaces X1, X2, X3 belong to set X (data points)

    • Binary or real-valued feature vector X of word occurrences

    • d features (words and other things, d is approximately 100,000)

  • Class Y

    • Spam = 1

    • Ham = -1

2. Linear models for classification#

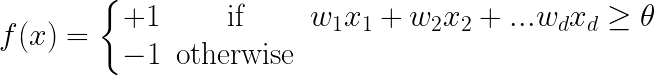
../_images/017.png

  • Vector Xj contains real values

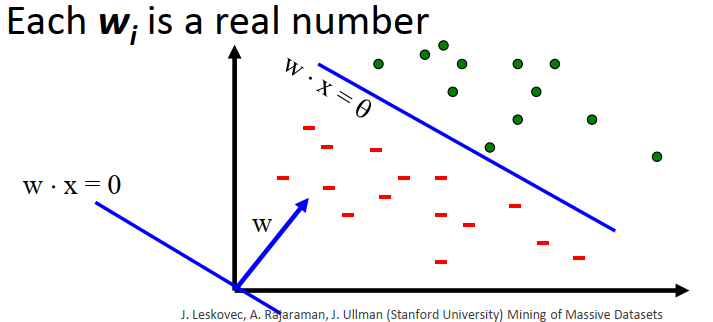
  • The goal is to find a vector W = (w1, w2, …, wd) with wj is a real number such that:

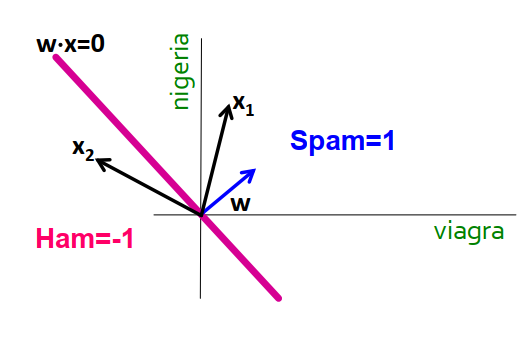
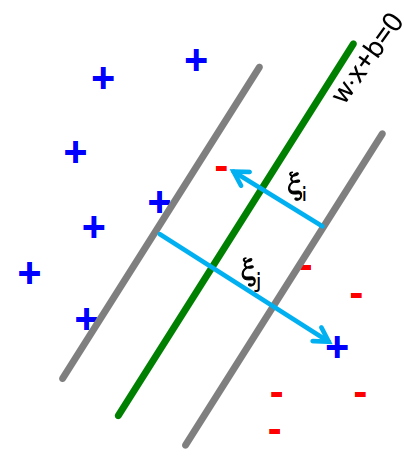
    • The labeled points are clearly separated by a line:

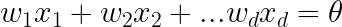
../_images/026.png

  • Dot is spam, minus is ham!

../_images/035.png

3. Linear classifiers#

  • Each feature i as a weight wi

  • Prediction is based on the weighted sum:

../_images/044.png

  • If f(x) is:

    • Positive: predict +1

    • Negative: predict -1

../_images/053.png

4. Support Vector Machine#

  • Originally developed by Vapnik and collaborators as a linear classifier.

  • Could be modified to support non-linear classification by mapping into high-dimensional spaces.

  • Problem statement:

    • We want to separate + from - using a line.

    • Training examples:

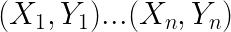
../_images/062.png

  • Each example i:

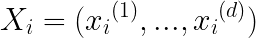
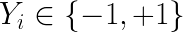
../_images/072.png ../_images/082.png

  • Inner product:

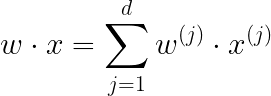
../_images/092.png

  • Which is the best linear separate defined by w?

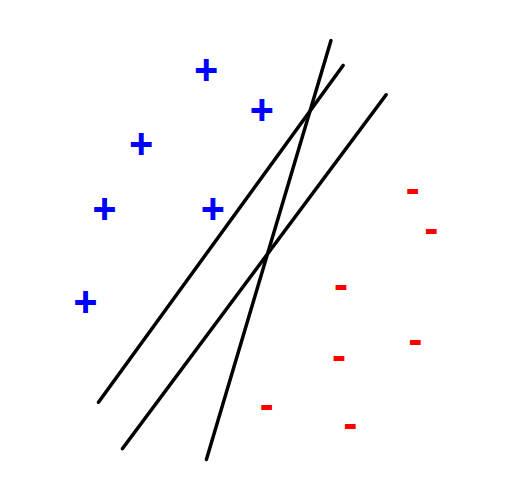
../_images/102.png

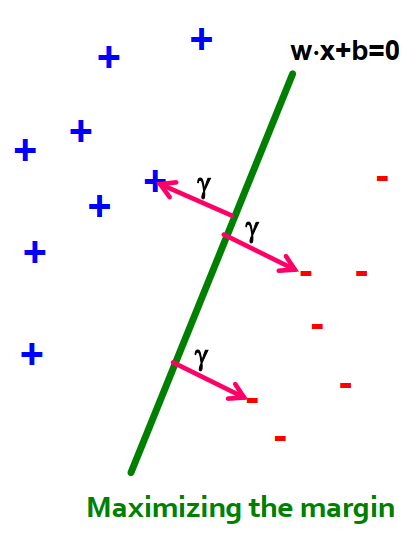
5. Support Vector Machine: largest margin#

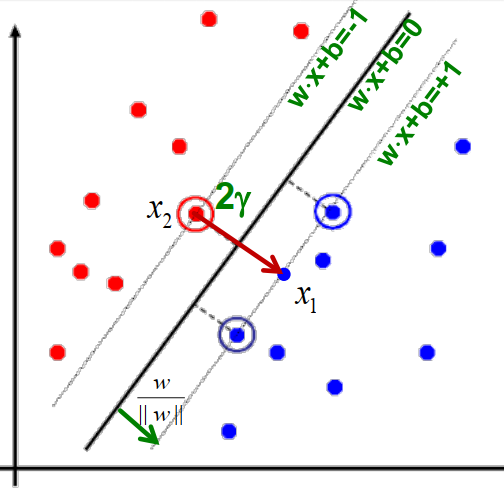
  • Distance from the separating line corresponds to the confidence of the prediction.

  • For example, we are more sure about the class of A and B than of C.

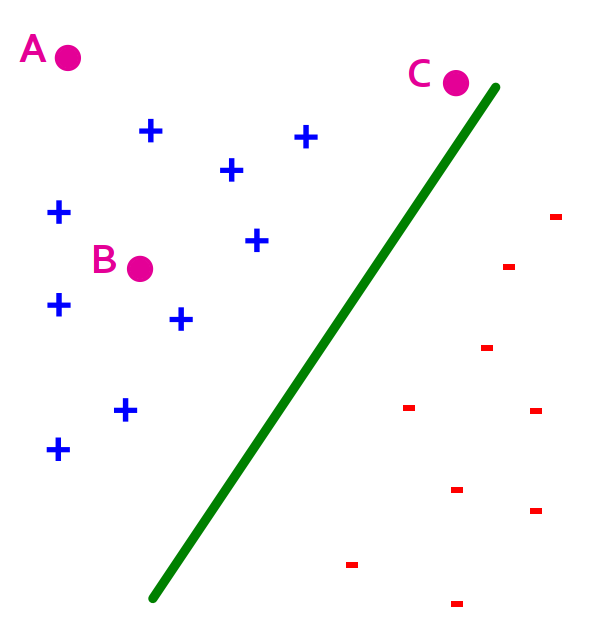
../_images/111.png

  • Margin definition:

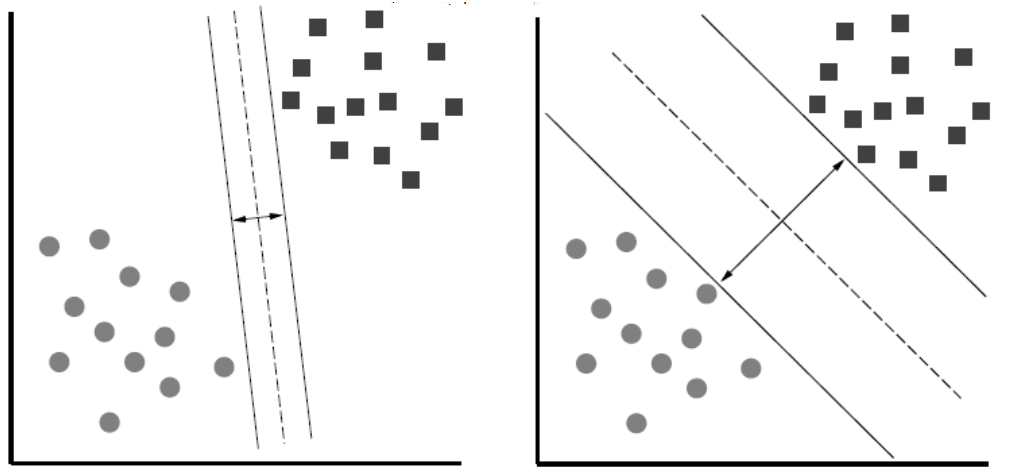
../_images/121.png ../_images/13.png

  • Maximizing the margin while identifying w is good according to intuition, theory, and practice.

../_images/14.png

  • A math question: how do you narrate this equation?

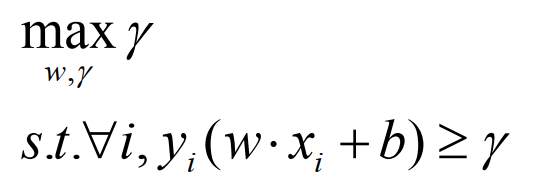
../_images/15.png

6. Support Vector Machine: what is the margin?#

  • Slide from the book

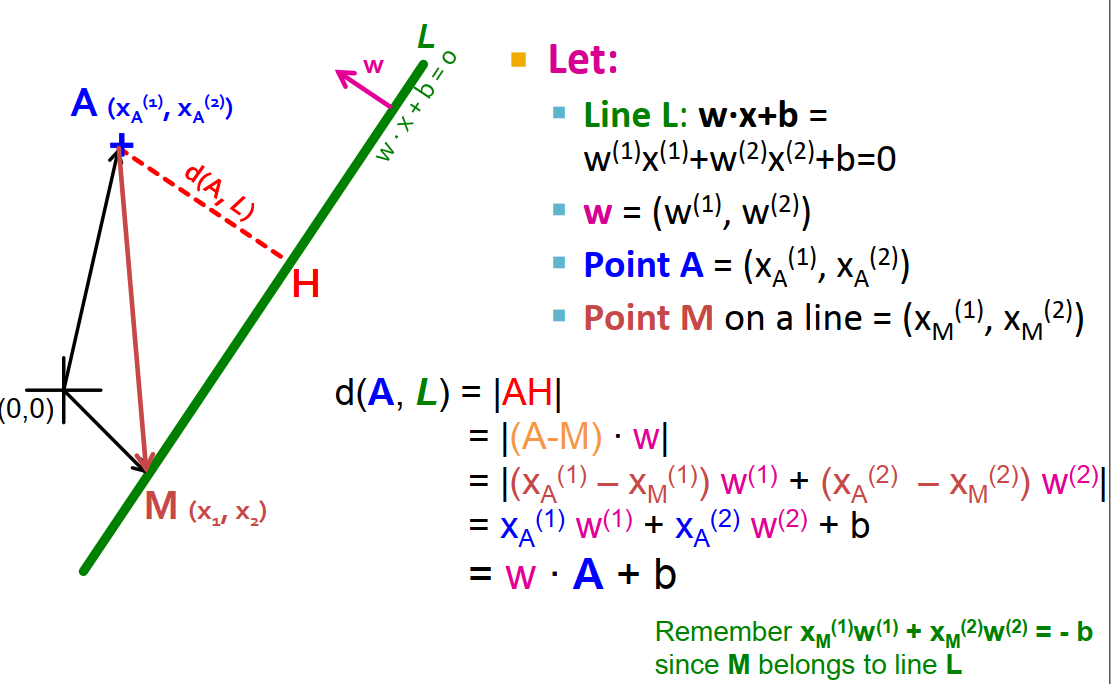
../_images/16.png

  • Notation:

    • Gamma is the distance from point A to the linear separator L: d(A,L) = |AH|

    • If we select a random point M on line L, then d(A,L) is the projection of AM onto vector w.

    • Project

    • If we assume the normalized Euclidean value of w, |w|, is equal to one, that bring us to the result in the slide.

  • In other words, maximizing the margin is directly related to how w is chosen.

  • For the ith data point:

../_images/17.png

7. Some more math …#

../_images/18.png

  • After some more mathematical manipulations:

../_images/19.png

  • Everything comes back to an optimization problem on w:

../_images/20.png ../_images/21.png

8. SVM: Non-linearly separable data#

../_images/22.png

  • For each data point:

    • If margin greater than 1, don’t care.

    • If margin is less than 1, pay linear penalty.

  • Introducing slack variables:

../_images/23.png ../_images/24.png