MPI: pleasantly parallel and workload allocation#

1. Definition#

  • Embarrassingly/naturally/pleasantly parallel.

  • A computation that can obviously be divided into a number of completely different parts, each of which can be executed by a separate process.

  • Each process can do its tasks without any interaction with the other processes, therefore, …

    • No communication or very little communication among the processes.

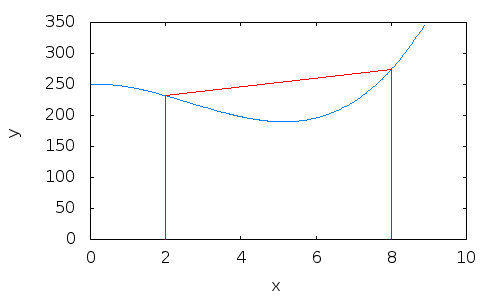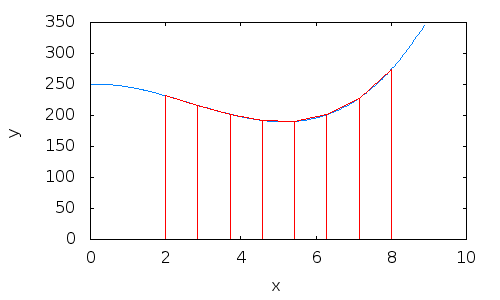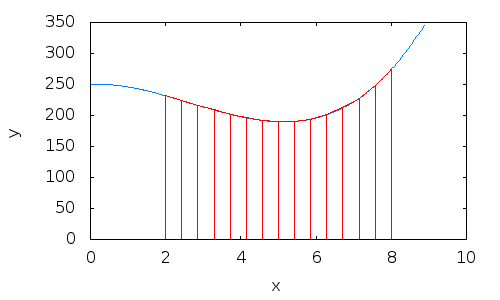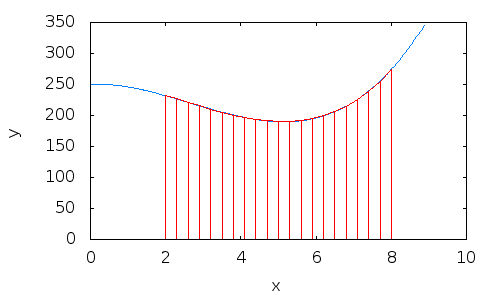
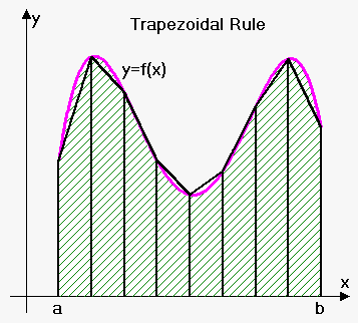
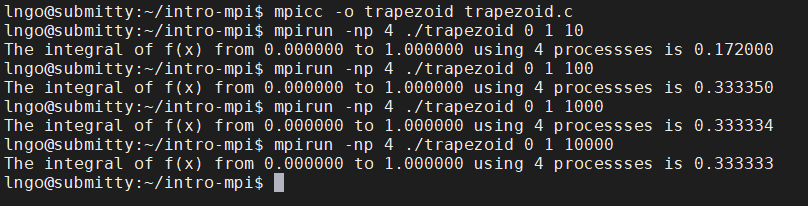
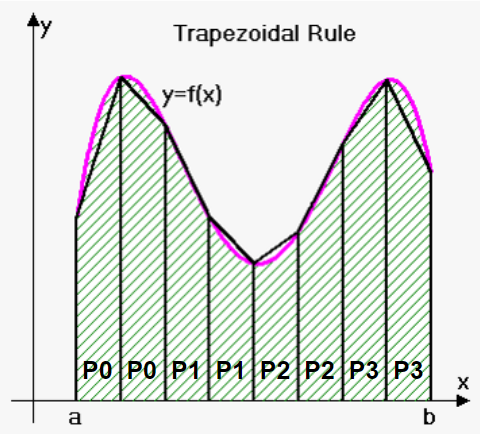
2. Example: integral estimation using the trapezoid method#

  • A technique to approximate the integral of a function f.

  • Integral is defined as the area of the region bounded by the graph f, the x-axis, and two vertical lines x=a and x=b.

  • We can estimate this area by dividing it into infinitesimal trapezoids.

trapezoids

3. Example: integral estimation using the trapezoid method#

  • Divide the area under the curve into 8 trapezoids with equal base h.

    • N = 8

    • a = 0

    • b = 2

  • The base h can be calculated as:

    • h = (b - a) / N = 0.25

trapezoids

4. Example: integral estimation using the trapezoid method#

  • Which trapezoid (workload/task) goes to which process?

    • Start with small number of processes.

    • Calculation workload assignment manually for each count of processes.

    • Generalize assignment for process i based on sample calculations.

trapezoids

5. Example: integral estimation using the trapezoid method#

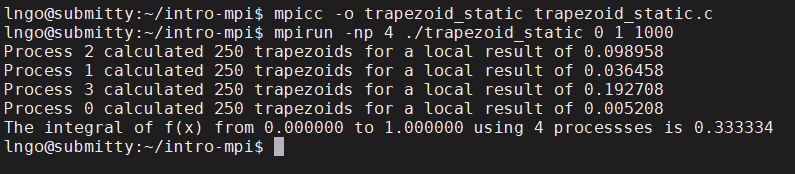
  • 4 processes: P0, P1, P2, P3: size = 4

  • N = 8

  • a = 0

  • b = 2

  • The height h can be calculated as:

    • h = (b - a) / N = 0.25

  • The amount of trapezoid per process:

    • local_n = N / size = 2;

  • local_a: variable represent the starting point of the local interval for each process. Variable local_a will change as processes finish calculating one trapezoid and moving to another.

    • local_a for P0= 0 = 0 + 0 * 2 * 0.25

    • local_a for P1= 0.5 = 0 + 1 * 2 * 0.25

    • local_a for P2= 1 = 0 + 2 * 2 * 0.25

    • local_a for P2= 1.5 = 0 + 3 * 2 * 0.25

trapezoids

6. Handson: integral estimation using the trapezoid method#

  • Inside intro-mpi, create a file named trapezoid.c with the following contents

  • Compile and run trapezoid.c:

$ mpicc -o trapezoid trapezoid.c
$ mpirun -np 4 ./trapezoid 0 1 10
$ mpirun -np 4 ./trapezoid 0 1 100
$ mpirun -np 4 ./trapezoid 0 1 1000
$ mpirun -np 4 ./trapezoid 0 1 10000
trapezoids

7. Hands-on: static workload assignment#

  • Is this fair?

  • Create a copy of trapezoid.c called trapezoid_static.c and modify trapezoid_static.c to have the following contents

  • Compile and run trapezoid_static.c:

$ mpicc -o trapezoid_static trapezoid_static.c
$ mpirun -np 4 ./trapezoid_static 0 1 1000
trapezoid static

  • This is called static workload assignment.

mandelbrot static

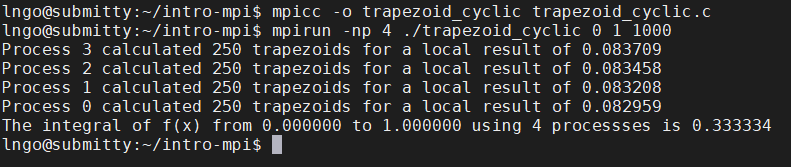
8. Hands-on: cyclic workload assignment#

  • Create a copy of trapezoid_static.c called trapezoid_cyclic.c and modify trapezoid_cyclic.c to have the following contents

  • Compile and run trapezoid_cyclic.c:

$ mpicc -o trapezoid_cyclic trapezoid_cyclic.c
$ mpirun -np 4 ./trapezoid_cyclic 0 1 1000
trapezoid cyclic

  • This is called cyclic workload assignment.

mandelbrot cyclic

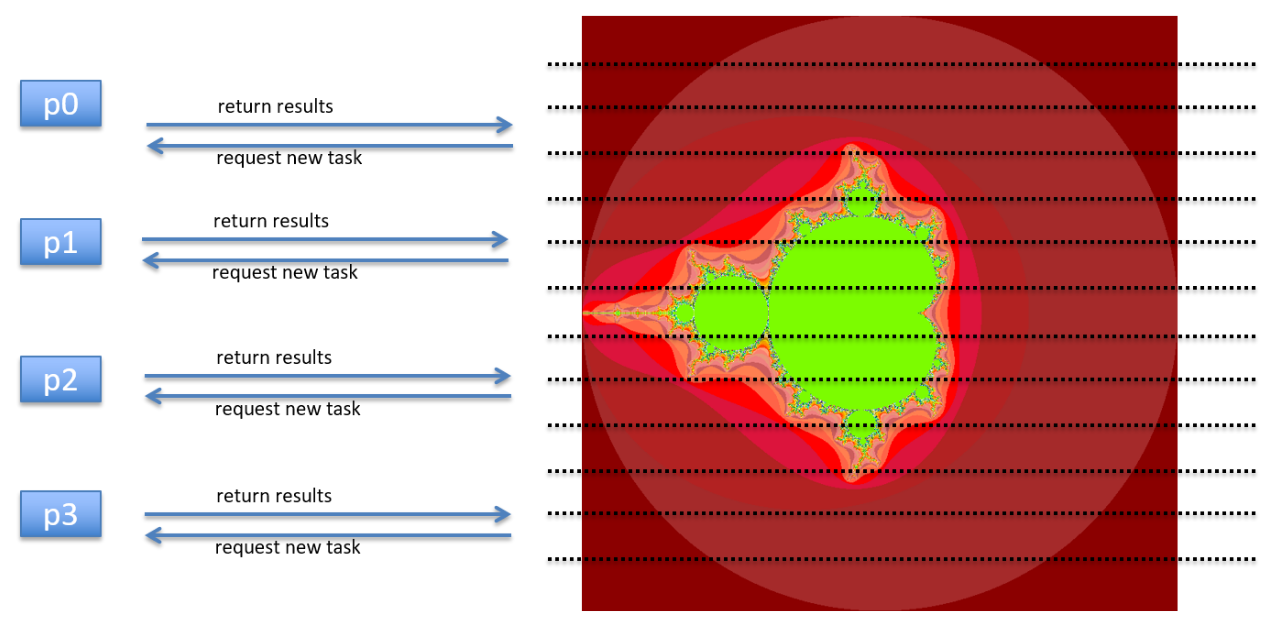
9. Hands-on: dynamic workload assignment#

  • Create a file called trapezoid_dynamic_.c with the following contents:

  • Compile and run trapezoid_dynamic.c:

$ mpicc -o trapezoid_dynamic trapezoid_dynamic.c
$ mpirun -np 4 ./trapezoid_dynamic 0 1 1000
$ mpirun -np 4 ./trapezoid_dynamic 0 1 1000
$ mpirun -np 4 ./trapezoid_dynamic 0 1 1000

{: .language-bash}

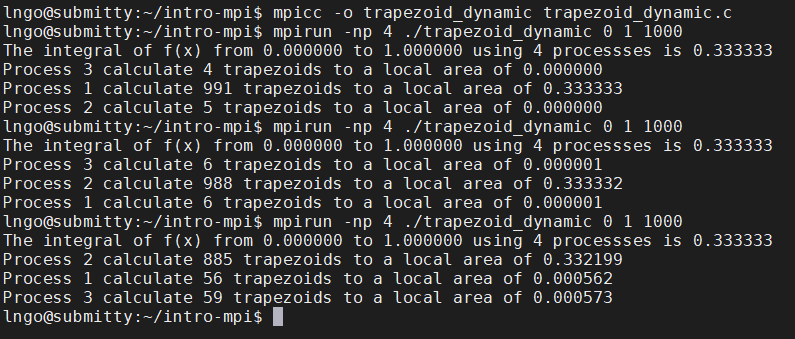
trapezoid dynamic

  • This is called dynamic workload assignment.

mandelbrot dynamic