Locality Sensitive Hashing

1. Applications of set-similarity

Many data mining problems can be expressed as finding similar sets:

• Pages with similar words, e.g., for classification by topic.

• NetFlix users with similar tastes in movies, for recommendation systems.

• Dual: movies with similar sets of fans.

• Entity resolution.

2. Application: similar documents

Given a body of documents, e.g., the Web, find pairs of documents with a lot of text in common, such as:

• Mirror sites, or approximate mirrors.

  • Application: Don’t want to show both in a search.

• Plagiarism, including large quotations.

• Similar news articles at many news sites.

  • Application: Cluster articles by same story: topic modeling, trend identification.

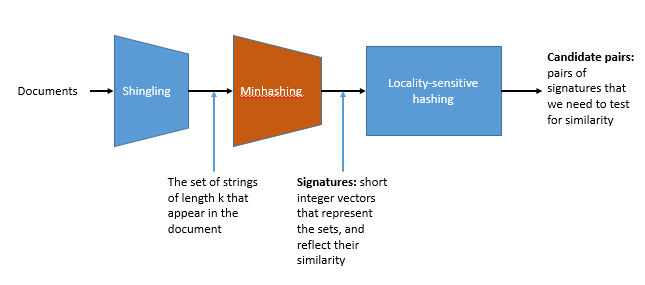
3. Three essential techniques for similar documents

• Shingling : convert documents, emails, etc., to sets.

• Minhashing : convert large sets to short signatures, while preserving similarity.

• Locality sensitive hashing : focus on pairs of signatures likely to be similar.

4. Shingles

• A k-shingle (or k-gram) for a document is a sequence of k characters that appears in the document.

• Example: k = 2; doc = abcab. Set of 2-shingles: {ab, bc, ca}.

• Represent a doc by its set of k-shingles.

• Documents that are intuitively similar will have many shingles in common.

• Changing a word only affects k-shingles within distance k from the word.

• Reordering paragraphs only affects the 2k shingles that cross paragraph boundaries.

• Example: k=3, The dog which chased the cat versus The dog that chased the cat.

  • Only 3-shingles replaced are g_w, _wh, whi, hic, ich, ch_, and h_c.

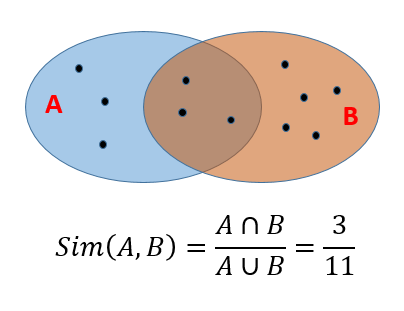
5. Minhashing: Jaccard Similarity

• The Jaccard similiarity of two sets is the size of their intersection divided by the size of their union.

• Convert from sets to boolean matrices.

  • Rows: elements of the universal set. In other words, all elements in the union.

  • Columns: individual sets.

  • A cell value of 1 in row e and column S if and only if e is a member of S.

  • A cell value of 0 otherwise.

  • Column similarity is the Jaccard similarity of the sets of their rows that have the value of 1.

  • Typically sparse.

• This gives you another way to calculate similarity: column similarity = Jaccard similarity.

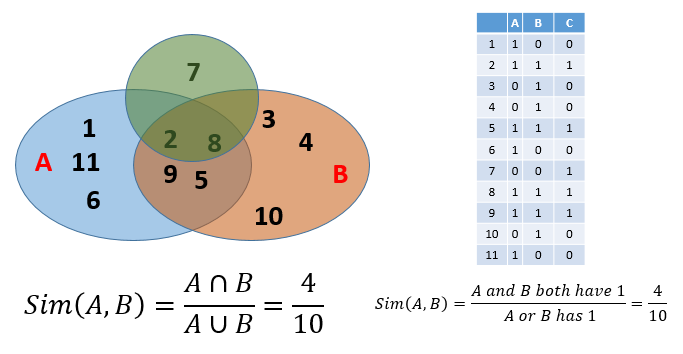
• Generally speaking, given two columns, rows maybe classified as:

  • a: 1 1

  • b: 1 0

  • c: 0 1

  • d: 0 0

• Sim(C₁, C₂) = a/(a+b+c)

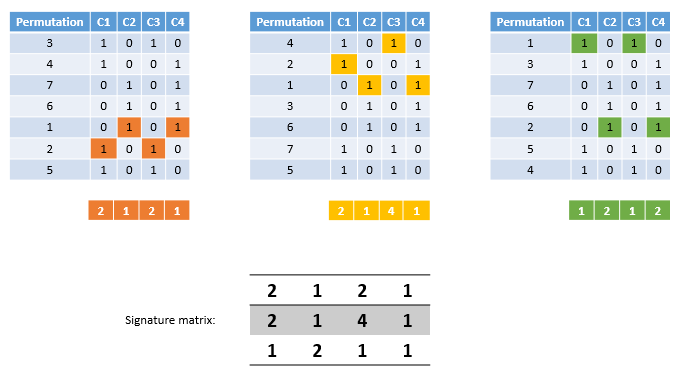
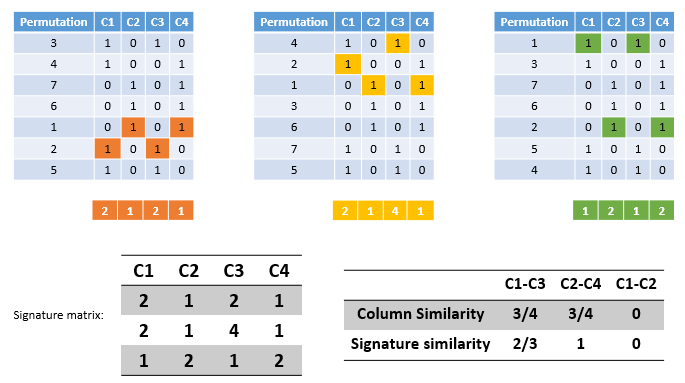
6. Minhashing

• Imagine the rows permuted randomly.

• Define minhash function h(C) = the number of the first (in the permuted order) row in which column C has 1.

• Use several (e.g., 100) independent hash functions to create a signature for each column.

• The signatures can be displayed in another matrix called the signature matrix

• The signature matrix has

  • its columns represent the sets and

  • the rows represent the minhash values, in order for that column.

6. Minhashing: surprising property

• The probability (over all permutations of the rows) that h(C₁) = h(C₂) is the same as Sim(C₁).

• Both are a/(a+b+c)!

• The similarity of signatures is the fraction of the minhash functions in which they agree.

• The expected similarity of two signatures equals the Jaccard similarity of the columns.

  • The longer the signatures, the smaller the expected error will be.

8. Hands-on Minhashing: implementation

• Can’t realistically permute billion of rows:

  • Too many permutation entries to store.

  • Random access on big data (big no no).

• How to calculate hashes in sequential order?

  • Pick approximately 100 hash functions (100 permutations).

  • Go through the data set row by row.

  • For each row r, for each hash function i,

    • Maintain a variable M(i,c) which will maintain the smallest value value of h_i(r) for which column c has 1 in row r.

9. Minhashing:

• Create three additional row permutations, update the signature matrix, and recalculate the signature similarity.

• Does the signature similarity become closer to the column similarity?

10. Locality-sensitive-hashing (LSH)

• Generate from the collection of signatures a list of candidate pairs: pairs of elements where similarity must be evaluated.

• For signature matrices: hash columns to many buckets and make elements of the same bucket candidate pairs.

  • Pick a similarity threshold t, a fraction < 1.

  • We want a pair of columns c and d of the signature matrix M to be a candidate pair if and only if their signatures agree in at least fraction t of the rows.

11. LSH

• Big idea: hash columns of signature matrix M several times and arrange that only similar columns are likely to hash to the same bucket.

• Reality: we don’t need to study the entire column.

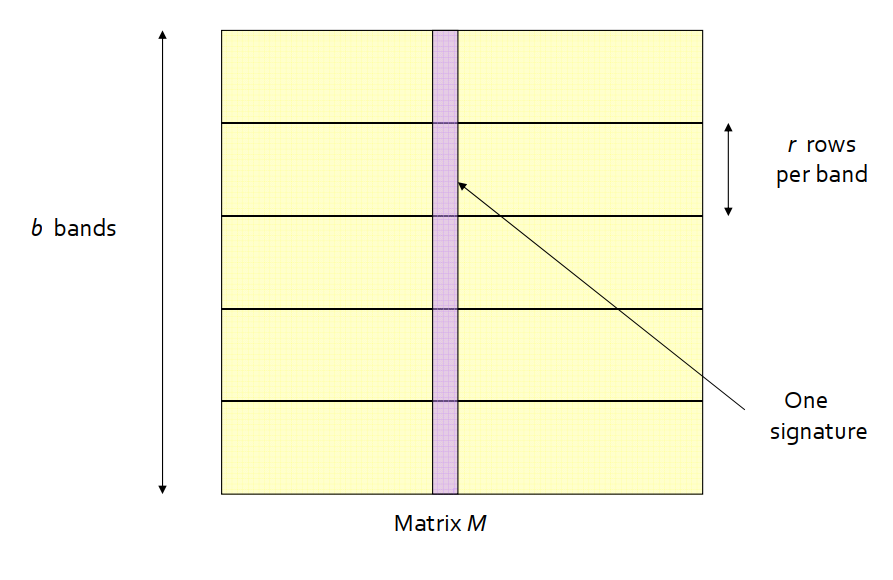
• Divide matrix M into b bands of r rows each.

• For each band, hash its portion of each column to a hash table with k buckets, with k as large as possible.

• Candidate column pairs are those that hash to the same bucket for at least one band.

• Fine tune b and r.

• We will not go into the math here …

12. Hands on LSH

• Download the set of inaugural speeches from https://www.cs.wcupa.edu/lngo/data/inaugural_speeches.zip.

• Launch a Spark notebook and create the two initial setup cells.