Page Rank
Contents
Page Rank#
1. Web page organization in the past#
Web pages were manually curated and organized.
Does not scale.

Next, web search engines were developed: information retrieval
Information retrieval focuses on finding documents from a trusted set.

Challenges for web search:
Who to trust given the massive variety of information sources?
Trustworthy pages may point to each other.
What is the best answer to a keyword search (given a context)?
Pages using the keyword in the same contexts tend to point to each other.
All pages are not equally important.
Web pages/sites on the Internet can be represented as a graph:
Web pages/sites are nodes on the graph.
Links from one page to another represents the incoming/outgoing connections between nodes.
We can compute the importance of nodes in this graph based on the distribution/intensity of these links.
2. PageRank: initial formulation#
Link as votes:
A page (node) is more important if it has more links.
Incoming or outgoing?
Think of incoming links as votes.
Are all incoming links equals?
Links from important pages count more.
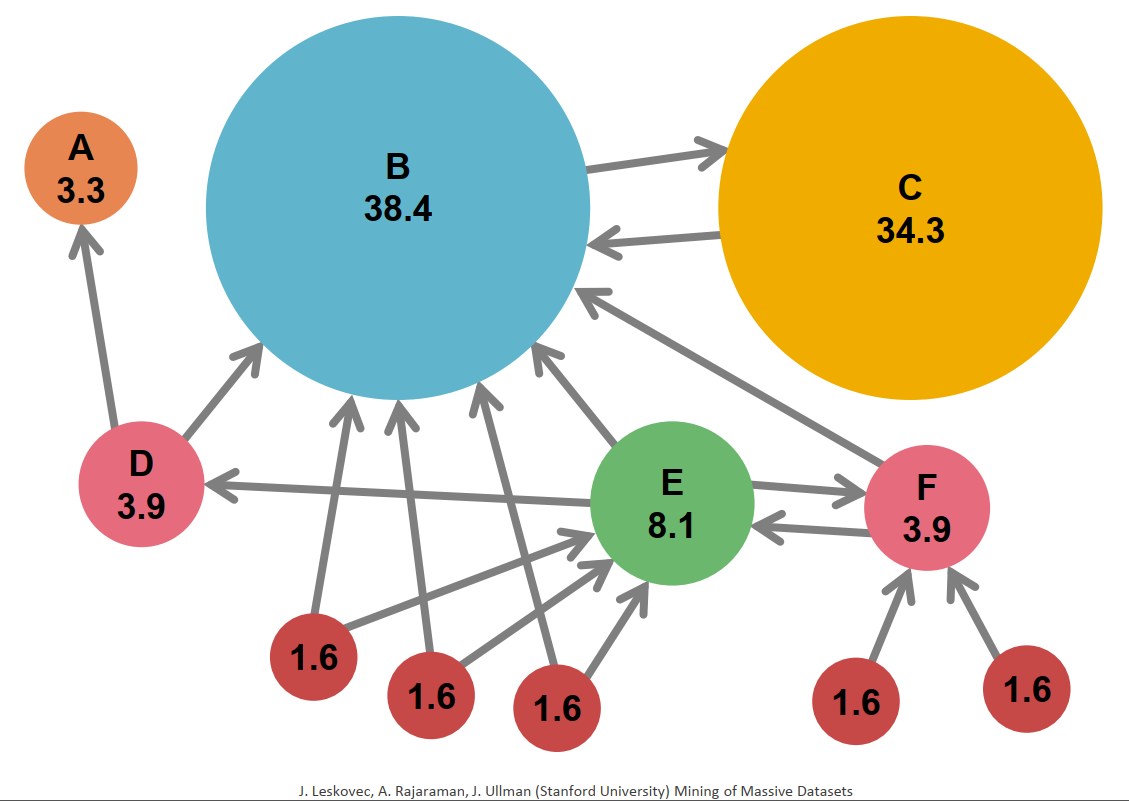
Each link’s vote is proportional to the importance of its source page.
If page j with importance rj has n outgoing links, each outgoing link has rj/n votes.
The importance of page j is the sum of the votes on its incoming links.
3. PageRank: the flow model#
Summary:
A
votefrom an important page is worth more.A page is important if it is linked to by other important pages.
Flow equations:
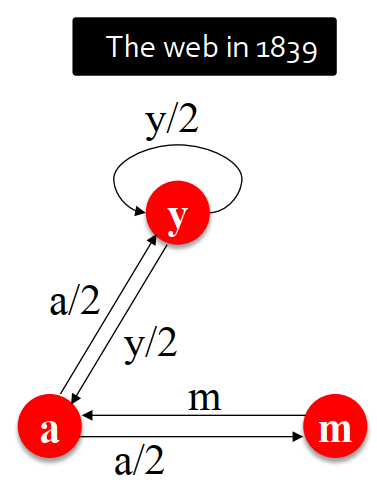
ry = ry/2 + ra/2
ra = ry/2 + rm
rm = ra/2
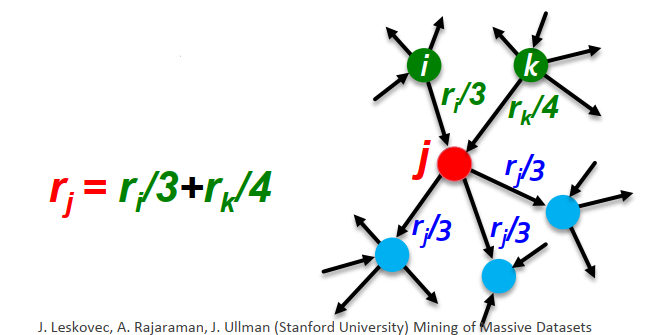
General equation for calculating rank rj for page j:
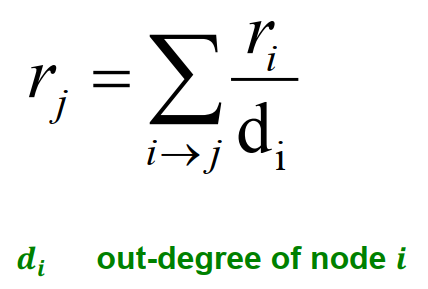
Three equations (actually two), three unknown.
No unique solutions
Additional constraint to force uniqueness:
ry + ra + rm = 1
Gaussian elimination:
ry = 2/5, ra = 2/5, rm = 1/5
Does not scale to Internet-size!
4. PageRank: matrix formulation#
Setup the flow equations as a stochastic adjacency matrix M
Matrix M of size N: N is the number of nodes in the graph (web pages on the Internet).
Let page i has *di outgoing links.
If there is an outgoing link from i to j, then
Mij = 1/di
else Mij = 0
Stochastic: sum of all values in a column of M is equal to 1.
Adjacency: non-zero value indicates the availability of a link.
Rank vector r: A vector with an entry per page.
The order of pages in the rank vector should be the same as the order of pages in rows and columns of M.

Flow equations:
ry = ry/2 + ra/2
ra = ry/2 + rm
rm = ra/2
General equation for calculating rank rj for page j with regard to all pages:
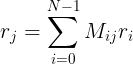
This can be rewritten in matrix form:
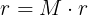
Visualization:
Suppose page i has importance *ri and has outgoing links to three other pages, including page j.
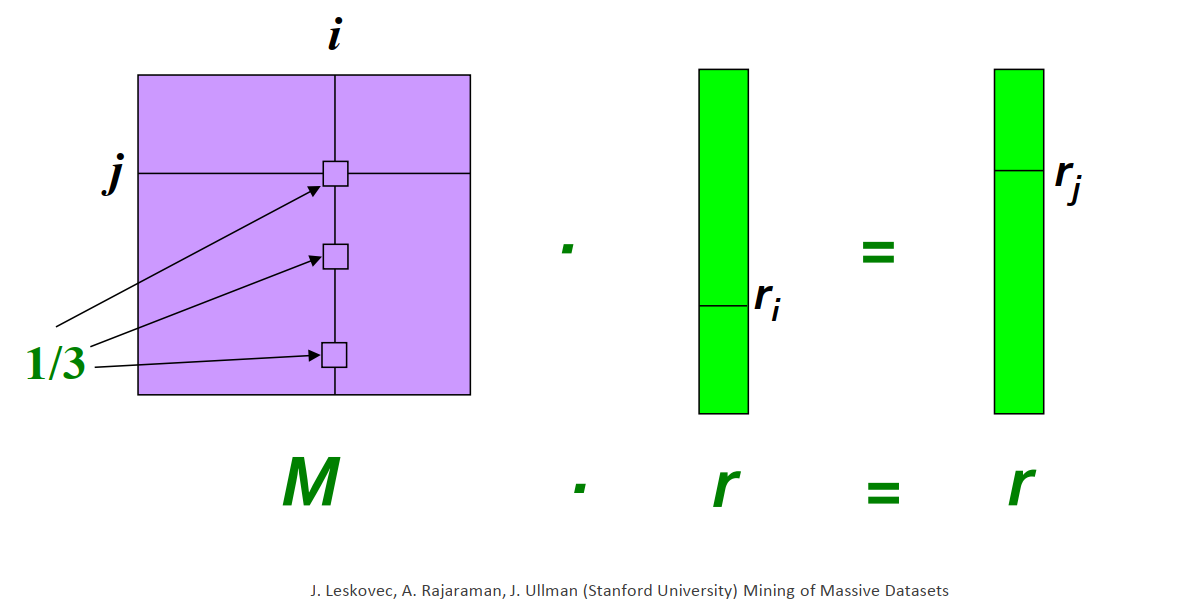
Final perspective:
Also, this is why we need to study advanced math …

5. PageRank: power iteration#
We want to find the page rank value r
Power method: an iterative scheme.
Support there are
Nweb pages on the Internet.All web pages start out with same importance:
1/N.Rank vector r: r(0) = [1/N, …,1/N]T
Iterate: r(t+1) = M • r
Stopping condition: r(t+1) - r(t) < some small positive error threshold e.
Example:


6. PageRank: the Google formulation#
Challenge 6.1: Does it converge:#
Challenge 6.2: Does it converge to what we want?:#
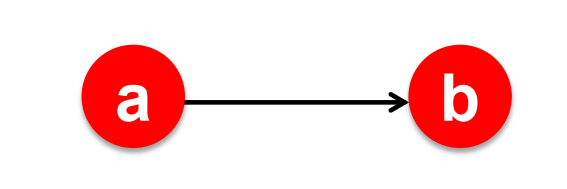
The
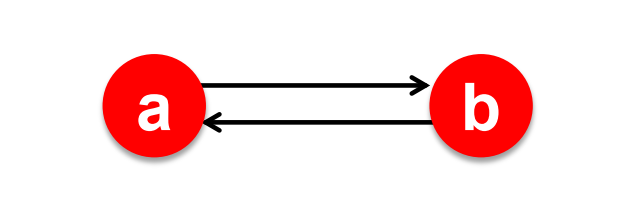
dead endproblemBuild the stochastic adjacency matrix for the following: graph and calculate the ranking for
aandb.
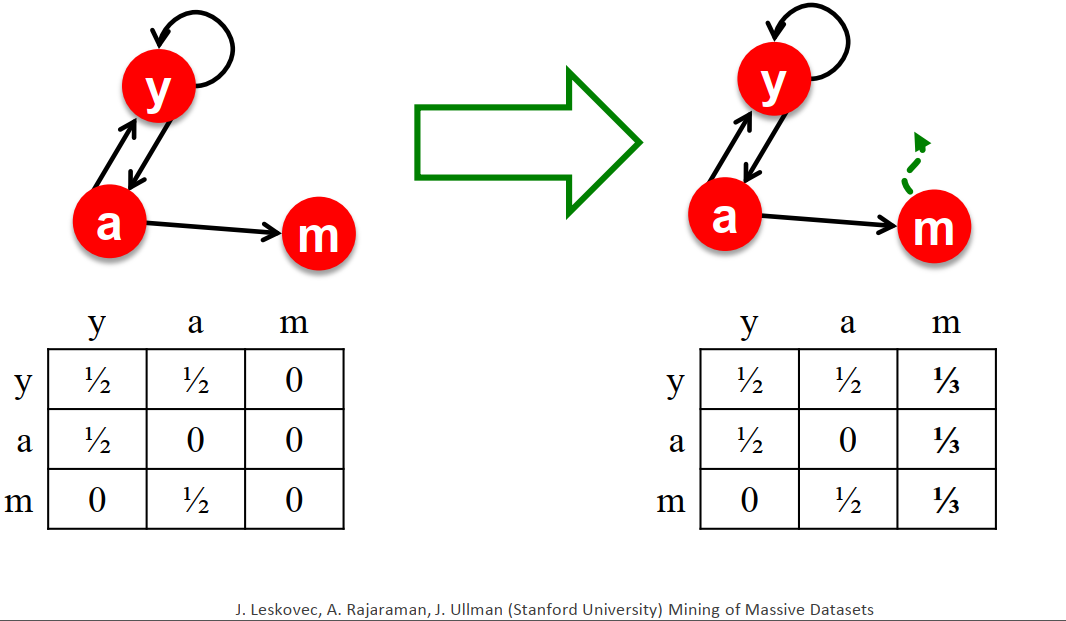
The solution: random teleport.
At each time step, the random surfer has two options:
A probably of β to follow an out-going link at random.
A probably of 1 - β to jump to some random page.
The value of β are between 0.8 to 0.9.
The surfer will teleport out of the spider trap within a few time steps.
The surfer will definitely teleport out of the dead-end.
Final equation for PageRank:
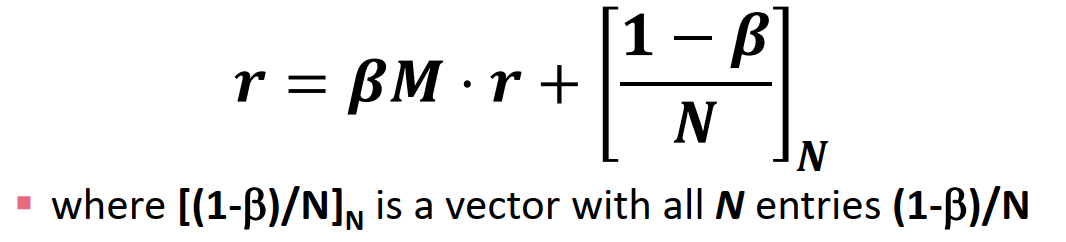
7. Hands-on: Page Rank in Spark#
Create a file called
small_graph.datwith the following contents:
y y
y a
a y
a m
m a
This data file describes the graph in the easlier slides.
8. Hands-on: Page Rank in Spark - Hollins dataset#
Import the Hollins dataset into your Kaggle.
Hollins University webbot crawl in 2004.
Which page is most important (internally).