Partitioning: Divide and Conquer

1. Partitioning

Partitioning simply divides the problem into parts and then compute the parts and combine results

• The basis of all parallel programming, in one form or another.

• Pleasantly parallel used partitioning without any interaction between the parts.

• Most partitioning formulation require the results of the parts to be combined to obtain the desired results.

• Partitioning can be applied to the program data.

  • This is call data partitioning or domain decomposition.

• Partitioning can also be applied to the functions of a program.

  • This is called functional decomposition.

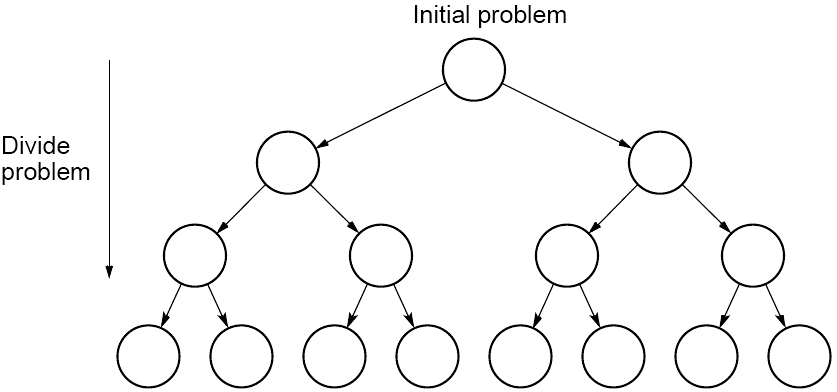
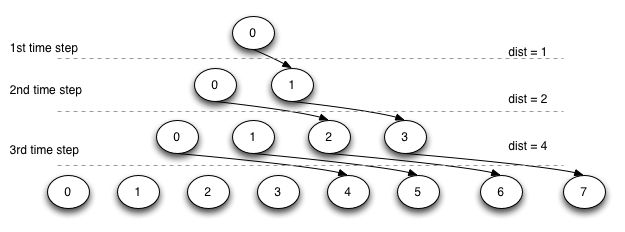
2. Divide and Conquer

• Characterized by dividing problem into sub-problems of same form as larger problem. Further divisions into still smaller sub-problems, usually done by recursion.

• Recursive divide and conquer amenable to parallelization because separate processes can be used for divided pairs. Also usually data is naturally localized.

Divide

• Create a file called divide.c

• Compile and run

$ mpicc -lm -o divide divide.c
$ mpirun -np 8 divide

Challenge: divide array

Create a copy of divide.c called divide_array.c that does the followings:

• Process 0 generates an 8-element array with random value populated.

  • Print out the contents of the array on a single line.

• Utilizing the tree communication approach in divide.c, send the data out to all remaining processes such as each process receives the value of the above array from the index position corresponding to that process’s rank.

Conquer

• Create a file called conquer.c

$ mpicc -lm -o conquer conquer.c
$ mpirun -np 8 conquer

Many sorting algorithms can be parallelized by partitioning using divide and conquer

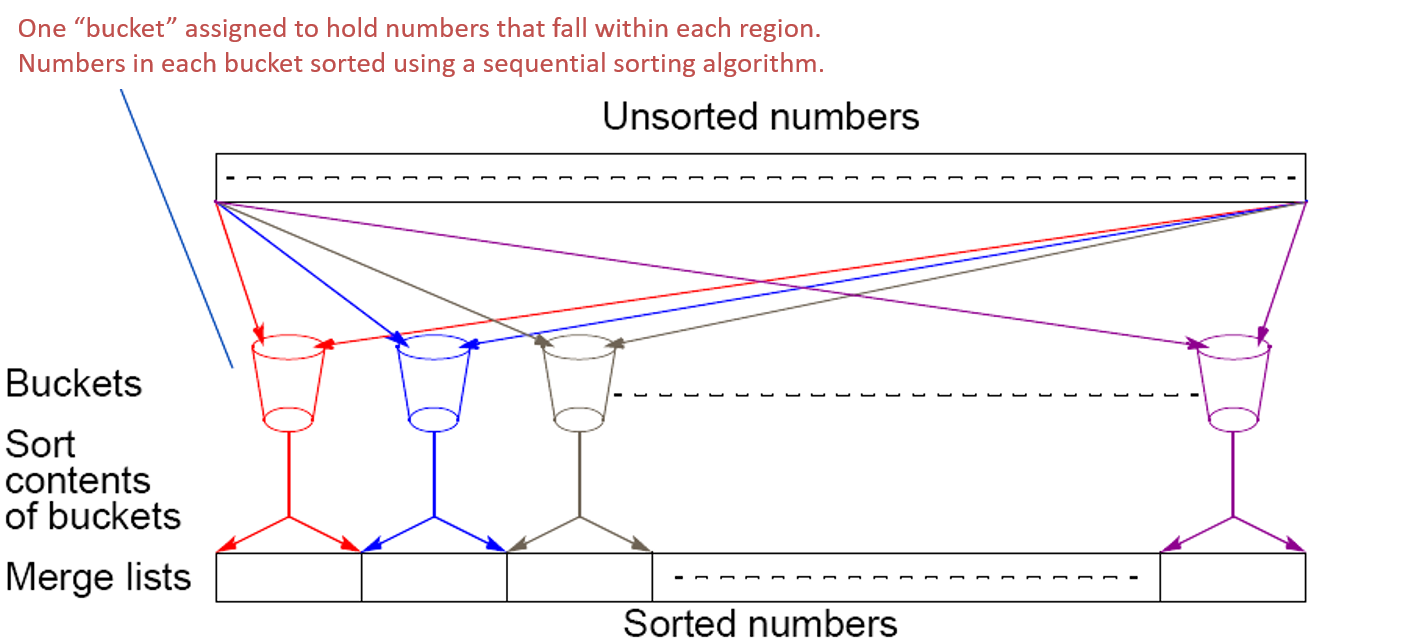
3. Bucket Sort

Overview

Parallel bucket sort: simple approach

• Broadcast data

• Sort only those elements that fit in local interval bucket (determined by rank)

• Gather sorted bucket

Scatter and Scatterv

int MPI_Scatter(
    void *sendbuf, 
    int sendcount, 
    MPI_Datatype sendtype, 
    void *recvbuf,
    int recvcnt,
    MPI_Datatype recvtype,
    int root, 
    MPI_Comm comm);

int MPI_Scatterv(
  void *sendbuf,
  int *sendcnts,
  int *displs,
  MPI_Datatype sendtype,
  void *recvbuf,
  int recvcnt,
  MPI_Datatype recvtype,
  int root,
  MPI_Comm comm
);

• sendbuf: address of send buffer (choice, significant only at root)

• sendcnts: integer array (of length group size) specifying the number of elements to send to each processor

• displs: integer array (of length group size). Entry i specifies the displacement (relative to sendbuf from which to take the outgoing data to process i

• sendtype: data type of send buffer elements

• recvbuf: address of receive buffer (choice)

• recvcnt: number of elements in receive buffer (integer)

• recvtype: data type of receive buffer elements

• root: rank of sending process (integer)

• comm: communicator

Hands-on: Scatterv

mpicc -o scatterv scatterv.c
mpirun -np 4 scatterv

Gather and Gatherv

int MPI_Gather(
    void *sendbuff, 
    int sendcnt, 
    MPI_Datatype sendtype, 
    void *recvbuff,
    int recvcnt,
    MPI_Datatype recvtype,
    int root, 
    MPI_Comm comm);

int MPI_Gatherv(
  void *sendbuf,
  int sendcnt,
  MPI_Datatype sendtype,
  void *recvbuf,
  int *recvcnts,
  int *displs,
  MPI_Datatype recvtype,
  int root,
  MPI_Comm comm
);

• sendbuf: starting address of send buffer (choice)

• sendcnt: number of elements in send buffer (integer)

• sendtype: data type of send buffer elements

• recvbuf: address of receive buffer (choice, significant only at root)

• recvcnts: integer array (of length group size) containing the number of elements that are received from each process (significant only at root)

• displs: integer array (of length group size). Entry i specifies the displacement relative to recvbuf at which to place the incoming data from process i (significant only at root)

• recvtype: data type of recv buffer elements (significant only at root)

• root: rank of receiving process (integer)

• comm: communicator

Hands-on: Gatherv

mpicc -o gatherv gatherv.c
mpirun -np 4 gatherv

Parallel bucket sort: simple approach implementation

mpicc -o bucket1 bucket1.c
mpirun -np 8 bucket1

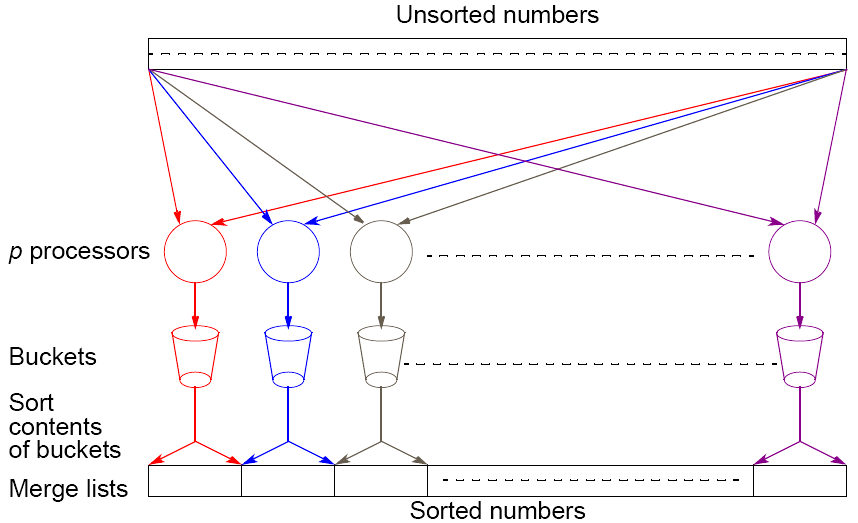
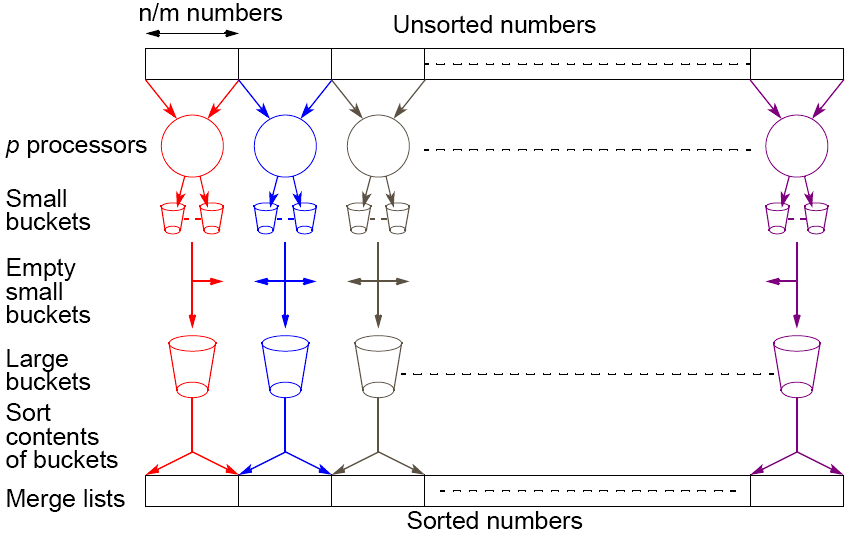
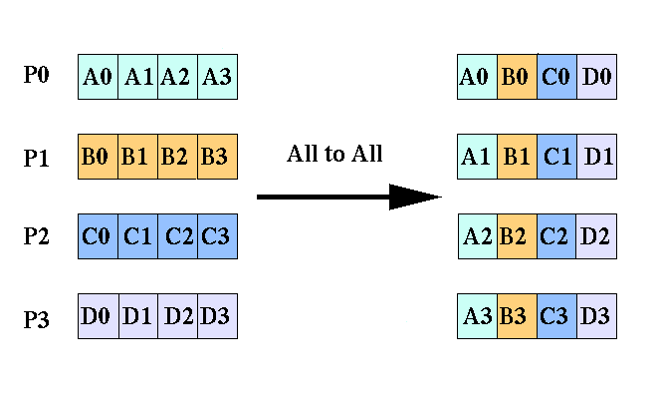
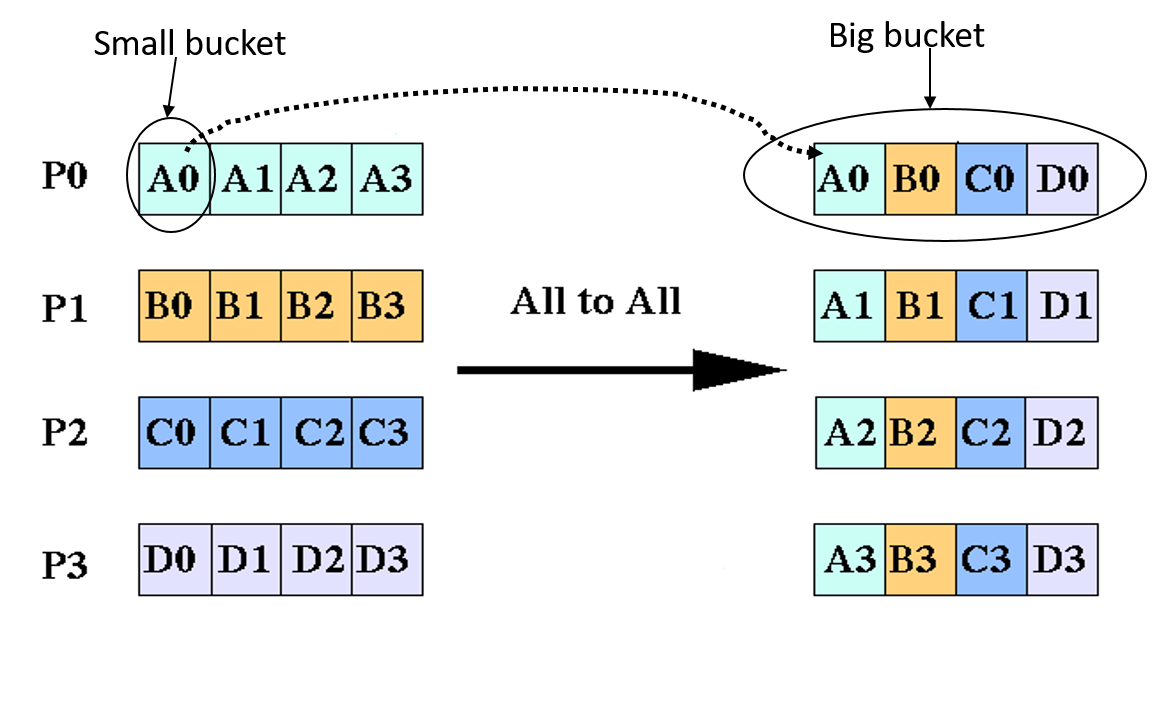
Parallel bucket sort: complex approach

• The data might be too large to be distributed via MPI_Bcast

• The necessary communication pattern: all to all

Alltoall

int MPI_Alltoall(
  void *sendbuf,
  int sendcount,
  MPI_Datatype sendtype,
  void *recvbuf,
  int recvcount,
  MPI_Datatype recvtype,
  MPI_Comm comm
);

• sendbuf: starting address of send buffer (choice)

• sendcount: number of elements to send to each process (integer)

• sendtype: data type of send buffer elements

• recvbuf: address of receive buffer (choice)

• recvcount: number of elements received from any process (integer)

• recvtype: data type of receive buffer elements

• comm: communicator

Hands-on: Alltoall

mpicc -o alltoall alltoall.c 
mpirun -np 4 alltoall

Alltoallv

int MPI_Alltoallv(
  void *sendbuf,
  int *sendcnts,
  int *sdispls,
  MPI_Datatype sendtype,
  void *recvbuf,
  int *recvcnts,
  int *rdispls,
  MPI_Datatype recvtype,
  MPI_Comm comm
);

• sendbuf: starting address of send buffer (choice)

• sendcnts: integer array equal to the group size specifying the number of elements to send to each processor

• sdispls: integer array (of length group size). Entry j specifies the displacement (relative to sendbuf from which to take the outgoing data destined for process j

• sendtype: data type of send buffer elements

• recvbuf: address of receive buffer (choice)

• recvcnts: integer array equal to the group size specifying the maximum number of elements that can be received from each processor

• rdispls: integer array (of length group size). Entry i specifies the displacement (relative to recvbuf at which to place the incoming data from process i

• recvtype: data type of receive buffer elements

• comm: communicator

Hands-on: Alltoallv

mpicc -o alltoallv alltoallv.c 
mpirun -np 4 alltoallv

Parallel bucket sort: complex approach implementation

mpicc -o bucket2 bucket2.c
mpirun -np 8 bucket2

4. N-Body Problem

Overview

** Fundamental settings for most, if not all, of computational simulation problems: **

• Given a space

• Given a group of entities whose activities are (often) bounded within this space

• Given a set of equation that governs how these entities react to one another and to attributes of the containing space

• Simulate how these reactions impact all entities and the entire space overtime

• Computation requires parallelization

• Experimental spaces are simulated at massive scale (millions of entities)

• Individual time steps are significantly smaller than the total simulation time.

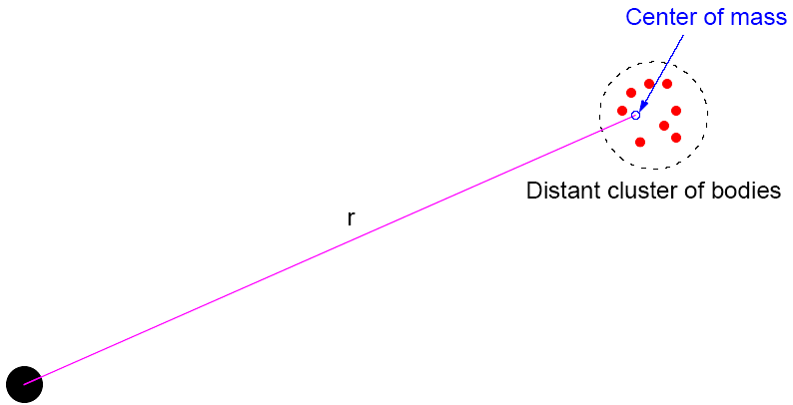
• Time complexity can be reduced by approximating a cluster of distant bodies as a single distant body with mass sited at the center of the mass of the cluster

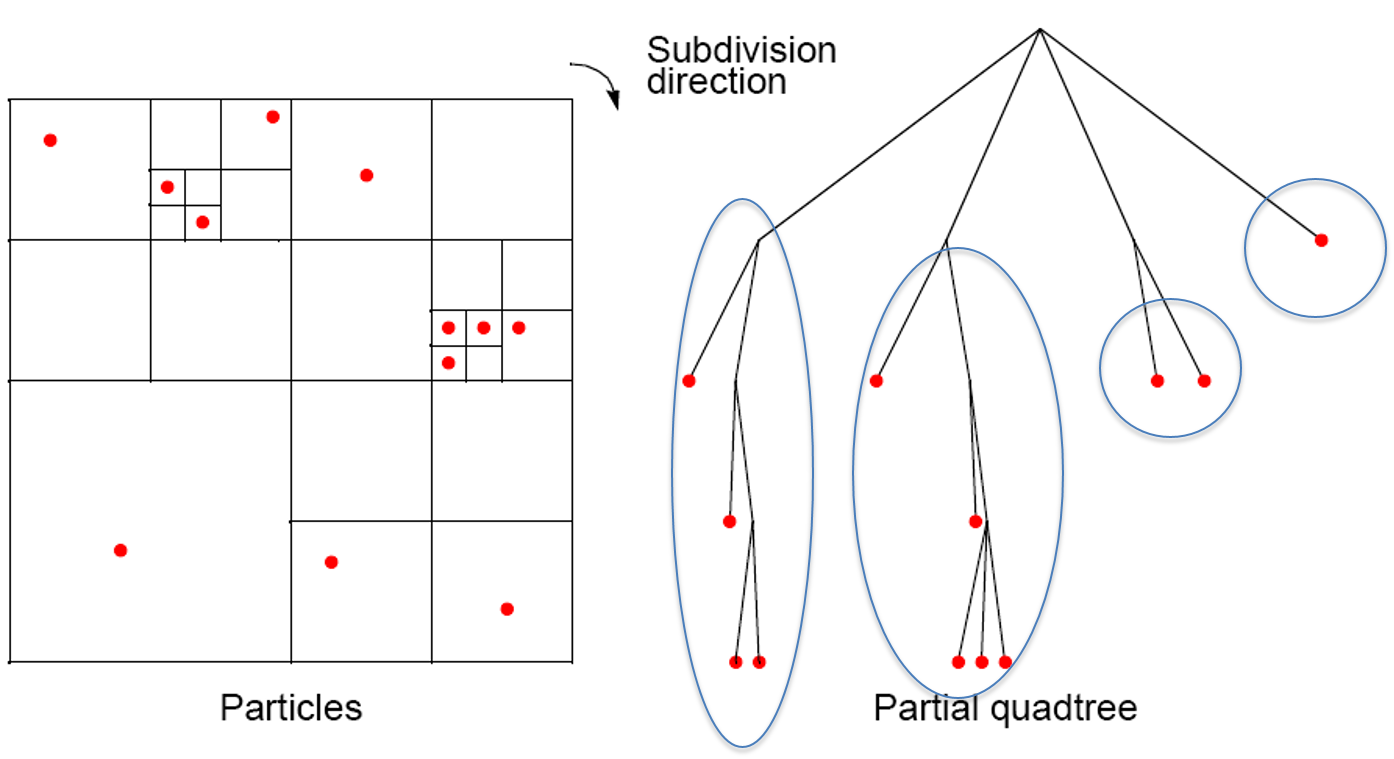
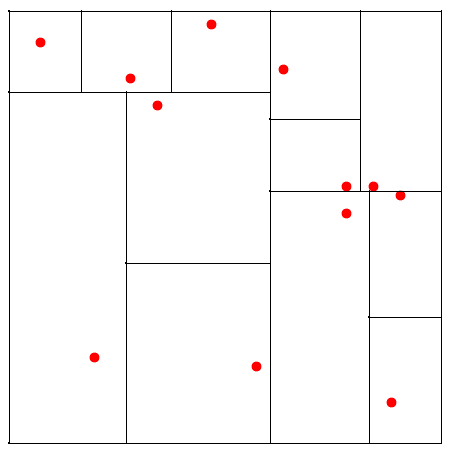
Barnes-Hut Algorithm (2-D)

Start with whole region in which one square contains the bodies (or particles).

• First, this cube is divided into four subregions.

• If a subregion contains no particles, it is deleted from further consideration.

• If a subregion contains one body, it is retained.

• If a subregion contains more than one body, it is recursively divided until every subregion contains one body.

• Create an quadtree – a tree with up to four edges from each node

• The leaves represent cells each containing one body.

• After the tree has been constructed, the total mass and center of mass of the subregion is stored at each node.

Orthogonal Recursive Bisection

• First, a vertical line found that divides area into two areas each with equal number of bodies.

• For each area, a horizontal line found that divides it into two areas, each with equal number of bodies.

• Repeated as required.